AI leren

Figuur 1: Schematische weergave van ANN

Figuur 2: Schematische weergave van een verbonden ANN. De invoer in dit netwerk bestaat uit twee elementen. Er zijn twee verborgen lagen, de eerste met drie knopen en de tweede met twee knopen. Er is in dit voorbeeld slechts één output.

Figuur 3: Een knoop in een neuraal netwerk wordt een perceptron genoemd.

In de inleiding neurale netwerken van de sectie technieken heb je kennis gemaakt met de structuur van een kunstmatig neuraal netwerk (figuur 1) die is opengewerkt in figuur 2. Een neuraal netwerk bestaat uit een invoerlaag, verborgen lagen en een uitvoerlaag. De verborgen lagen en de uitvoerlaag zijn opgebouwd uit knopen ofwel perceptrons (figuur 3), ook wel neuronen of knopen genoemd. Iedere percepton verwerkt de inkomende signalen tot een uitvoer door de inkomende signalen te wegen en het gewogen resultaat door te geven aan een ontvanger (volgende knoop of gebruiker). Tijdens het trainen van het netwerk wordt naar de meest passende wegingsfactoren gezocht. We gaan nu proberen het leerproces van een neuraal netwerk te verduidelijken en beginnen met het meest simpele netwerk waarmee we toch nog wat complexiteit kunnen duiden, een netwerk bestaande uit één perceptron met twee invoeren en één uitvoer. We gebruiken hier de trainingsvorm begeleid leren (=supervised learning).

De werking van een perceptron

Een perceptron volgt het "feed-forward"-model. Dit betekent dat inputs naar het neuron worden gestuurd, worden verwerkt en resulteren in een output, de stroom van informatie is dus in één richting. In het bovenstaande diagram betekent dit dat het netwerk (één neuron) van links naar rechts leest: inputs komen binnen, worden verwerkt en als output doorgegeven.

Laten we eens de verschillende stappen bekijken.

Het leren van de perceptron

Stap 1: Ontvang invoer.

Stel dat we een perceptron hebben met twee ingangen - laten we ze $x_{1}$ en $x_{2}$ noemen en als voorbeeld de volgende waarden geven:

$\mathbf{Invoer 1}: x_{1} = 12$
$\mathbf{Invoer 2}: x_{2} = 4$

Stap 2: Gewicht invoer.

Bekijk nogmaals figuur 3. Elke invoer die naar een neuron wordt gestuurd, moet eerst worden gewogen, d.w.z. worden vermenigvuldigd met een bepaalde gewichtsfactor. Zoals boven al is gemeld, moeten juist die gewichtsfactoren door training worden bepaald. Bij het maken van een perceptron beginnen we meestal met het toewijzen van willekeurige gewichten. Laten we hier de invoer de volgende gewichten ($w_{1}$ en $w_{2}$) geven:

$\mathbf{Gewicht 1}: w_{1} = 0.5$
$\mathbf{Gewicht 2}: w_{2} = -1$

We nemen elke invoer en vermenigvuldigen deze met het bijbehorende gewicht:

$\mathbf{Gewicht 1} \cdot \mathbf{Invoer 1} = x_{1} \cdot w_{1} = 12 \cdot 0.5 = 6$
$\mathbf{Gewicht 2} \cdot \mathbf{Invoer 2} = x_{2} \cdot w_{2} = 4 \cdot -1 = -4$

Stap 3: Tel alle bijdragen op.

De gewogen invoer worden vervolgens opgeteld:

$\mathbf{Som} = x_{1} \cdot w_{1} + x_{2} \cdot w_{2} = 6 + -4 = 2$

Stap 4: Genereer uitvoer.

Activeringsfuncties: De tekenfunctie heeft alleen de waarden -1,0,1 als uitvoer. De sigmoïde functie $sig(x)=\frac{1}{1 + e^{-x}}$ stijgt van 0 naar 1. De tangens hyperbolicus functie $\tanh(x)$ stijgt van -1 naar 1. Al deze activeringsfuncties zijn puntsymetrisch in het snijpunt met de $y$-as. Dit is van belang in het trainingsproces van een netwerk. Je ziet dat de $\tanh$ functie een gladdere versie is van de tekenfunctie.

De uitvoer (output) van een perceptron wordt gegenereerd door de som uit de vorige stap door een activeringsfunctie te laten gaan. In het geval van een binaire uitvoer, is het de activeringsfunctie die bepaalt op basis van de waarde van de som of deze moet “vuren” of niet. Je kunt je een LED voorstellen die is aangesloten op het uitgangssignaal van de perceptron: als hij vuurt, gaat het licht aan; zo niet, dan blijft het uit.

Activeringsfuncties zijn er in verschillende vormen, simpele maar ook voor de leek moeilijker te begrijpen wiskundige functies. Voor ons eerste perceptron model houden we het zo simpel mogelijk. De activeringsfunctie die we hier kiezen is het teken van de waarde van de som. Met andere woorden, als de som een positief getal is, is de uitvoer 1, als het negatief is, is de uitvoer -1. In netwerken met meerdere lagen kan deze teken activeringsfunctie niet worden gebruikt om het netwerk te trainen (zie stap 4 in het trainingsproces dat verder op in dit hoofdstuk wordt behandeld). In de figuur hiernaast zie je behalve de teken functie nog de sigmoïde functie en de tangens hyperbolicus, deze activeringsfuncties gebruiken we in het volgende hoofdstuk.

$\mathbf{Uitvoer} = \mathbf{teken(som)} = \mathbf{teken(2)} = 1 $

Samengevat hebben we het volgende algoritme dat we hierna gaan programmeren.

Het Perceptron Algoritme:

Vermenigvuldig elke invoer met het gewicht bij deze invoer.
Bepaal de som van al deze gewogen waarden.
Bereken de uitvoer van de perceptron gebaseerd op deze som met behulp van de activeringsfunctie (Hier het teken van de waarde van de som).

Coderen:

Als je de bovenstaande theorie zelf in javascript wilt programmeren klap dan dit blok uit.

We gaan ons perceptron algoritme in Javascript implementeren. In een andere taal kan dat natuurlijk ook. Neem het volgende html document als startpunt. Druk in de browser F12 om de uitvoer van console.log( ... ) te zien

<!DOCTYPE html>
<html>
  <head>
	<meta charset="UTF-8">
	<meta name="author" content="Jouw naam">
	<title>Neuraal netwerk: perceptron</title>
	<script type="text/javascript">
	   console.log("Druk in de browser op f12."+
				   "Je ziet dan in de tab console deze tekst");
	   var invoer    = [12 , 4]; // x1,x2
	   var gewichten = [0.5 , -1];  // w1,w2
	</script>
  <head>
  <body>
  </body>
</html>

Voeg nu code toe om de som van de gewogen invoer te berekenen en toon de som in de console.

Uitwerking

<!DOCTYPE html>
<html>
  <head>
    <meta charset="UTF-8">
    <meta name="author" content="Jouw naam">
    <title>Neuraal netwerk: perceptron</title>
    <script type="text/javascript">
       var invoer    = [12 , 4]; // x1,x2
       var gewichten = [0.5 , -1];  // w1,w2

       var som = 0;
       var i;
       for(i=0;i<invoer.length;i++)
       {
          som += invoer[i]*gewicht[i];
       }
       console.log("De gewogen som is "+som);
    </script>
  <head>
  <body>
  </body>
</html>

Gebruik nu de teken methode als activeringsfunctie of schrijf die zelf. En laat zien wat de uitvoer van de perceptron is.

Uitwerking

<!DOCTYPE html>
<html>
  <head>
    <meta charset="UTF-8">
    <meta name="author" content="Jouw naam">
    <title>Neuraal netwerk: perceptron</title>
    <script type="text/javascript">
       var invoer    = [12 , 4]; // x1,x2
       var gewichten = [0.5 , -1];  // w1,w2
       var som = 0;
       var i;
       for(i=0;i<invoer.length;i++)
       {
          som += invoer[i]*gewicht[i];
       }
       console.log("De gewogen som is "+som);
       uitvoer = Math.sign(som);
       console.log("De uitvoer ofwel het teken van de som is "+uitvoer);
    </script>
  <head>
  <body>
  </body>
</html>

Onderliggende lijn

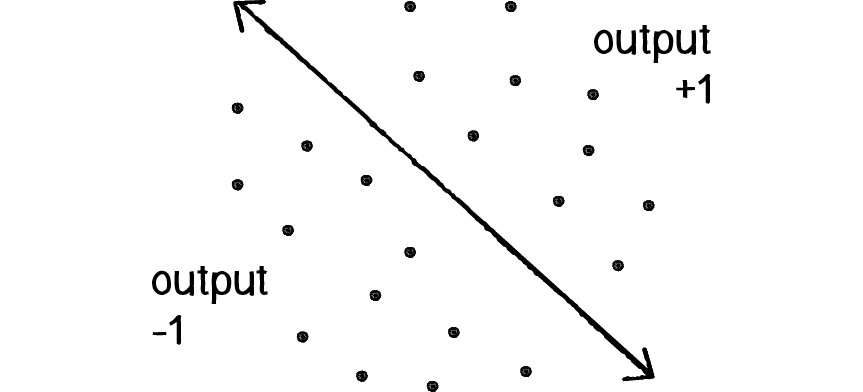
Figuur 4: Voorspel of een punt onder (output moet -1 zijn) of boven (output moet +1 zijn) de lijn ligt.

Figuur 5: de perceptron in het neurale netwerk voor de lijn bepaling.
Figuur 6: de uitvoer van de perceptron: +1 als som groter dan 0, -1 als som kleiner dan 0. Vul een punt in (inclusief bias) en druk op de knop. Voor de uitleg van de grafiek zie de tekst.

Nu we het rekenproces van een perceptron begrijpen, gaan we deze met een herkenbaar voorbeeld in actie zetten. We hadden al gemeld dat neurale netwerken vaak worden gebruikt voor patroonherkenningstoepassingen, zoals gezichtsherkenning. Bij patroonherkenningstoepassingen wordt gezocht naar de klasse waartoe een patroon hoort. Zelfs met onze eenvoudige perceptron kunnen we de basisprincipes van classificatie demonstreren. In het volgende voorbeeld (figuur 4) gaan we, met slechts één perceptron, een scheidingslijn proberen te vinden tussen een regio -1 en +1. Om het netwerk te trainen, gebruiken we straks een verzameling punten met $x$- en $y$-coördinaten, in combinatie met de gewenste output per punt.

Je zou kunnen denken aan het zoeken van een kaarsrechte grens tussen twee grondsoorten. Aan één kant van de grens zit klei in de ondergrond, aan de andere kant zand. Er worden grondboringen verricht. Als er klei naar bovenkomt dan geven we dit monster de waarde 1, als er zand wordt aangeboord de waarde -1.

We beschouwen dus een lijn in een tweedimensionale ruimte (Zie figuur 4). Punten in die ruimte kunnen worden ingedeeld in een groep van punten die aan de ene kant van een lijn liggen en een groep aan de ander kant. Hoewel dit een ietwat dom voorbeeld is (we kunnen namelijk heel makkelijk bepalen of een punt onder of boven een lijn ligt), laat het voorbeeld zien hoe een perceptron getraind kan worden om punten aan de ene kant versus de andere te herkennen. Geven we het getrainde netwerk als invoer een $x$- en $y$-coördinaat dan moet het ons vertellen aan welke kant van de lijn dit punt ligt, zonder dat de vergelijking direct aan de perceptron wordt gegeven. Bovendien zal je zien dat in het trainingsproces de gewichten wel een heel speciale waarde krijgen.

We beginnen met het netwerk in figuur 3. Ofwel een neuraal netwerk met twee keer een invoer, één perceptron en één uitvoer gelijk aan de uitvoer van deze perceptron. De twee ingangen zijn de $x$- en $y$-coördinaten van een punt. Met behulp van een teken activeringsfunctie is de uitvoer -1, 0 of +1 — dat wil zeggen, de invoergegevens worden ingedeeld volgens het teken van de uitvoer. In figuur 4 kunnen we zien hoe elk punt zich onder de lijn (-1) of boven de lijn (+1) of op de lijn (0) bevindt.

Bias

We hebben met slechts twee invoeren wel een groot probleem. Als we het punt (0,0) aan dit netwerk voeren, dan is de gewogen som van de invoer altijd 0, want
$\mathbf{som} = x \cdot w_{1}+y \cdot w_{2} = 0 \cdot w_{1} + 0 \cdot w_{2}=0$.
Omdat de meeste lijnen niet door de oorsprong kan dit recept in het algemeen niet werken.

Om dit probleem te vermijden, heeft onze perceptron een derde input nodig, die wordt de bias (=afwijking) input genoemd. Een bias-input heeft altijd de waarde 1 en wordt ook gewogen. Hiernaast is in figuur 5 onze perceptron met de toegevoegde bias input weergegeven. De som wordt dan:
$\mathbf{som} = w_{0} + x \cdot w_{1}+y \cdot w_{2}$.
De som voor het punt (0,0) is dan:
$\mathbf{som} = w_{0} + 0 \cdot w_{1}+0 \cdot w_{2} = w_{0} $
ofwel het gewicht van de bias. Het gewicht $w_{0}$ bepaalt na training dus of (0,0) boven of onder de lijn ligt.

Nadat de som is berekend wordt in dit voorbeeld de uitvoer berekent met de teken activeringsfunctie.

$\mathbf{teken}(\mathbf{som})= 1$ als $som \gt 0$,
$\mathbf{teken}(\mathbf{som})= -1$ als $som \lt 0$ en
$\mathbf{teken}(\mathbf{som})= 0$ als $som = 0$

In de applet in figuur 6 kun je de uitvoer van een realisatie van onze perceptron laten uitrekenen, voor een punt $(x,y)$ vooraf gegaan door de input 1 voor de bias. Je kunt ook het punt verslepen om ervaren dat als je de lijn passeert het teken wisselt. Als je de knop "Maak nieuw perceptron" indrukt dan worden de gewichten $w_{0}, w_{1}, w_{2}$ opnieuw gekozen.

Waarom zie je in figuur 5 de rechte lijn? Deze rechte lijn is de weergave van de status van het perceptron. Deze status wordt gevormd door de waarden van de gewichten. Bekijk nogmaals de som

$$\mathbf{som} = w_{0} + x \cdot w_{1}+y \cdot w_{2}$$

en laten we eens kijken naar het geval dat de som nul is (dus ook $teken(som) = 0$ ).

$$0=w_{0}+x \cdot w_{1}+y \cdot w_{2}$$

Wat voor een vergelijking is dit?

antwoord
Dit is een vergelijking voor een rechte lijn. Herken je die niet in deze vorm kijk dan naar de volgende herleiding.
- Herleiding
  
  $\begin{array}{rcl} 0 & = & w_{0} + x \cdot w_{1}+y \cdot w_{2} \Rightarrow \\ - y \cdot w_{2} & = & x \cdot w_{1}+ w_{0} \Rightarrow \\ y & = & \frac{w_{1}}{-w_{2}} \cdot x + \frac{w_{0}}{-w_{2}} \\ y & = & a \cdot x + b \end{array}$
  Waarin $ a = \frac{w_{1}}{-w_{2}} $ en $ b = \frac{w_{0}}{-w_{2}} $

De gestippelde blauwe lijn in figuur 6 is dus de lijn die bij de perceptron hoort.

De code voor de perceptron in de applet vindt je onder de knop hieronder. Echter zonder de graphics. Wil je die ook bewaar dan dit document. In de code is het deel voor de perceptron gebundeld in een Javascript class Perceptron. Heb je nog nooit met Javascript classes gewerkt? In dat geval is onderstaand voorbeeld waarschijnlijk wel te volgen. Voor meer informatie over classes in Javascript kan je kijken op w3schools of je kan deze video bekijken.

Coderen:

Nieuwe code met Perceptron class

<html>
  <head>
    <script>
        
      const volgproces=false; // variabele wordt straks gebruikt om naar het console te schrijven
      var myPerceptron=null;  // myPerceptron object wordt straks gemaakt     
      // Het gebruik van objecten in javascript
      // wordt uitgelegd op https://www.w3schools.com/js/js_classes.asp
      
      // Definitie class Perceptron
      class Perceptron
      {
        /*
         * de methode constructor wordt aangeroepen als we straks
         * een Perceptron maken.
         * @param: n is het aantal inputs (inclusief de bias) die de perceptron krijgt
         * @param: f is de activeringsfunctie die de uitvoer bepaalt op basis van
		 *         de som van invoer keer gewichten f(som)
         */
        constructor(n,f) 
        {
          // Overal waar "this." voorstaat is een eigenschap
          // van een Perceptron object.
          // Sla het aantal knopen in een variabele op 
          this.aantalInvoerKnopen = n;
          // Sla de activeringsfunctie in een variabele op ;
          this.activeringsfunctie = f;
          // We maken nu een eerste gok voor de gewichten voor de Perceptron
          this.gewichten=[];
          // maak random gewichten voor het perceptron  
          for(var i=0;i<n;i++)
          {
            // Trek een toevalsgetal tussen 0 en 1. Door deze
            // met 2 te vermenigvuldigen en er 1 van af
            // te trekken wordt het dus een toevalsgetal tussen -1 en 1
            this.gewichten[i]=2*Math.random()-1; 
          }
        }
        /*
         * geefDoor is de feed-forward functie. De invoer [1,x1,...,xn]
         * wordt verwerkt tot de uitvoer
         */
        geefDoor(invoer)
        {
          var som =0;
          var i,uitvoer;
          // bepaal de som van de gewogen invoer
          for(i=0;i<this.aantalInvoerKnopen;i++)
          {
            som += invoer[i] * this.gewichten[i];
          }
          
          if(volgproces) console.log("De som van de gewogen invoer is "+ som);
          
          // verwerk de som met de activeringsfunctie
          return uitvoer = this.activeringsfunctie(som);
        }
      }
      //einde definitie Perceptron
      
      
	  
      // De vind lijn app code
      /*
       * functie maakPerceptron maakt een globaal Perceptron object myPerceptron
       * als die nog niet bestaat met n invoer knopen
       */
      function maakPerceptron(n,f)
      {
        if(myPerceptron==null) myPerceptron = new Perceptron(n,f);
      }
      
      /*
       * functie waarLigtPunt vraagt aan de perceptron in welk gebied het punt ligt
       * @param punt: [1, x-coördinaat , y - coördinaat ]
       */
      function waarLigtPunt(punt)
      {
        // Maak zo nodig de perceptron met de lengte van het punt en de teken functie
        if(myPerceptron==null)
        {
          maakPerceptron(invoer.length, Math.sign );
        }
		
        document.getElementById("uitvoer").innerHTML=
          "De output voor het punt " + punt + " is " + myPerceptron.geefDoor(punt);
      }
      // einde vind lijn app code
	  
    </script> 
  </head>
  <body>
    <button onclick="waarLigtPunt([1, 12 , 4])">Bereken de perceptron voor [1, 12 , 4]
    ofwel voor ht punt (x,y)=(12,4)</button>
    <p id="uitvoer"></p>
  </body>
</html>

Trainen van het netwerk

We hebben nu een perceptron die een voorspelling kan maken over de ligging van een punt $(x,y)$ ten opzichte vaneen lijn. Dit doet de perceptron door middel van de uitvoer functie geefDoor. Maar eigenlijk hebben we hier nog niks aan, de gewichten zijn namelijk willekeurig gekozen en toegewezen. We moeten het netwerk dus gaan trainen om het een goede voorspeller te laten zijn. In het trainingsproces is het de bedoeling dat het netwerk zelf tot een acceptabel resultaat komt. Afhankelijk van de complexiteit van een netwerk en de data zal dit trainen meer of minder moeite en dus ook tijd kosten. Daarover later meer.

Zoals eerder beloofd gebruiken we hier begeleid leren (supervised learning). We bieden de perceptron punten aan waarvan we weten wat de uitvoer is. Laten we nu eens kijken naar de essentiële stappen in het trainingsproces.

Stappen in het trainingsproces

Geef het netwerk invoer waarvoor het antwoord bekend is.
Vraag het netwerk om een antwoord bij die invoer.
Bereken de fout. (Was het antwoord van het netwerk goed of fout?)
Als er een fout is, pas dan de gewichten binnen het netwerk aan.
Ga terug naar stap 1 als er nog meer te trainen valt.

We passen begeleid leren toe. De trainer moet het netwerk (de leerling) van correcte voorbeelden voorzien, zodat het kan leren wat goed en fout is. Dit doen we in stap 1. Bijvoorbeeld bij punt (2,3) hoort uitvoer 1 en bij punt (0, 0) hoort uitvoer 0.

Stap 2 hebben we hierboven al behandeld, invoer [1, 2, 3] met de teken functie wordt omgezet in -1, 0 of 1 afhankelijk van de gewichten van de perceptron. Stel je geeft het punt (2, 3) aan de perceptron. Als de perceptron dan een uitvoerwaarde berekent die niet gelijk is aan 1, dan heeft de perceptron een fout gemaakt. Dit moeten we proberen te corrigeren zodat de perceptron de volgende keer hopelijk wel het goede antwoord geeft. Hiervoor moeten we eerst de fout berekenen.

Berekenen fout

De fout van een perceptron (of meer algemeen: netwerk) kan worden gedefinieerd als het verschil tussen het gewenste antwoord en zijn voorspelling.

FOUT = GEWENSTE OUTPUT - VOORSPELLING PERCEPTRON

In het geval van onze perceptron, met de teken functie als activeringsfunctie, heeft de uitvoer slechts drie mogelijke waarden: +1, 0, of -1. De mogelijke combinaties en de bijbehorende fouten staan in de tabel onder de knop. Zo is bijvoorbeeld bij een gewenste uitkomst 1 en voorspelling -1 de fout gelijk aan $1 - (-1) = 2$ en andersom bij een gewenste uitkomst -1 en voorspelling 1 is de fout gelijk aan $ (-1) - 1 = -2$

Foutentabel

Gewenst 1 1 1 0 0 0 -1 -1 -1

Voorspeld -1 0 1 -1 0 1 -1 0 1

fout 2 1 0 1 0 -1 0 -1 -2

Gewenst	1	1	1	0	0	-1	-1	-1
Voorspeld	-1	0	1	-1	1	-1	0	1
fout	2	1	0	1	-1	0	-1	-2

Aanpassen gewichten

Nu we de fout hebben berekend moeten we de gewichten aanpassen. De fout is de bepalende factor in hoe de gewichten van de perceptron moeten worden aangepast. Wat we voor een bepaald gewicht willen berekenen, is de verandering in dat gewicht, vaak $\Delta \mathbf{gewicht}$ genoemd (of "delta"-gewicht, waarbij delta de Griekse letter $\Delta$ is). Op basis van deze verandering bereken we een nieuw gewicht.

$\mathbf{nieuw}\,\mathbf{gewicht} = \mathbf{gewicht} + \Delta \mathbf{gewicht}$

$\Delta \mathbf{gewicht}$ wordt berekend door de fout te vermenigvuldigen met de invoer.

$\Delta \mathbf{gewicht} = \mathbf{fout}\,\cdot\,\mathbf{invoer}$.

De waarden van de nieuwe gewichten voor $w_0$, voor de bias, $w_1$, voor input x, en $w_2$, voor input y, worden dus bepaald op basis van waarde van de fout en de waarden van de invoer. Waarom werkt onze methode? We komen daar snel op terug.

Helaas zijn we er met bovenstaande regel nog niet helemaal. Omdat onze fout de waarden $-2,-1,0,1,2$ kan aannemen, kan het zijn dat $\Delta \mathbf{gewicht}$ te groot is en we over ons doel heen springen. We moeten het daarom mogelijk maken de snelheid van veranderen te kunnen sturen. We gebruiken daarvoor een factor $\mathbf{leersnelheid}$, zodat

$\Delta \mathbf{gewicht} = \mathbf{leersnelheid}\,\cdot\,\mathbf{fout}\,\cdot\,\mathbf{invoer}$.

Met deze laatste aanpassing is onze functie compleet en kunnen we het gaan toepassen in het leerproces van de perceptron.

De laatste stap, stap 5, van het trainingsproces is recursief (het proces wordt nog een keer aangeroepen). Als de gewichten zijn aangepast kan er worden gekeken of de voorspellingen van de perceptron voor de trainingsdata overeenkomen met de uitvoer van de trainingsdata, zo niet dan moet er verder worden getraind.

Overdenking trainingsstrategie

We hebben nu de regel om de gewichten van de perceptron te veranderen en leggen straks, met behulp van een wiskundige redevoering, uit waarom de regel werkt. Voor we dit doen proberen een beeld bij het trainen te schetsen.

In het begeleid leren wordt het netwerk gevoed met trainingsvoorbeelden waarbij bij een gegeven invoer de uitvoer bekend is. Deze uitvoer is in de ideale situatie correct, maar bij experimentele gegevens is dat hopelijk bij benadering waar. B.v. voor de quickdraw applicatie tekent iemand een kat. De intentie is een kat, maar de tekening lijkt eigenlijk net iets meer op een hond dan op een kat. Het plaatje gaat dan als kat de training van de applicatie in terwijl het eigenlijk als hond geclassificeerd had moeten worden. Als er teveel fouten aanwezig zijn dan kan er ook met AI geen waardevolle conclusies uit de dataset worden getrokken. Voorbeelden van andere fouten die kunnen optreden zijn bijvoorbeeld meetfouten in de invoer en of meetfouten in de uitvoer. Fouten in de trainingsdataset noemt men experimentele bias.

In het begeleid leren wordt het netwerk gevoed met trainingsvoorbeelden waarbij we vooronderstellen dat bij bekende invoer een bekende uitvoer aanwezig is. De manier van trainen in begeleid leren kan verschillen afhankelijk van de zekerheid van deze vooronderstellingen. Als zowel de invoer als de uitvoer volledig vast ligt kan men b.v. per trainingsvoorbeeld net zolang trainen tot het voorbeeld juist wordt voorspeld, dit is meestal efficiënter.

Als er echter foute of moeilijk te onderscheiden waarnemingen in de trainingsvoorbeelden zitten dan is dit geen goede strategie. Er moet een mogelijkheid voor het netwerk zijn om aan het trainingsvoorbeeld te kunnen "ontsnappen". Doe je dat niet dan kan zo'n fout invoer,uitvoer paar te zwaar meewegen in de berekeningen. Hierdoor kan het eindresultaat nooit helemaal correct voorspellingen doen, gezien het voorzien is van incorrecte of op elkaar gelijkende voorbeelden. Bij wijze van spreken kan zo’n fout paar niet in de grijze massa verdwijnen, maar is dan een dwingeland die met fake news zijn zin wil doordrijven. Als er fouten in de trainingsdata zijn (experimentele bias), dan zou het wiskundig het beste zijn om, vergelijkbaar met b.v. lineaire regressie, alle fouten die in de voorspellingen van het netwerk samen nemen en dan pas een aanpassing aan de gewichten van de perceptron te doen. Bij een grote trainingsdataset is dat echter weer lastig uit te voeren. Daarom wordt meestal gekozen voor het één keer aanpassen per datapunt, dit vervolgens voor alle datapunten te doen. Vervolgens kan deze hele reeks weer worden herhaald tot een aanvaardbaar niveau van de voorspellingen is bereikt.

Wiskundige onderbouwing waarom de regel voor de perceptron werkt.

Nu is het toch echt tijd om duidelijk te maken waarom de regel
$\mathbf{nieuw}\,\mathbf{gewicht} = \mathbf{gewicht} + \mathbf{leersnelheid}\,\cdot\,\mathbf{fout}\,\cdot\,\mathbf{invoer}$
werkt.
Er zijn meerdere manieren om dit te doen. Wij bekijken een manier die weinig wiskundige kennis vergt, namelijk vanuit de fouten tabel. Omdat de kans heel klein is dat we een punt precies op de lijn vinden, bekijken we alleen de situatie dat de fout -2, 0 of 2 is.

Als de fout 0 is dan is $\mathbf{leersnelheid}\,\cdot\,\mathbf{fout}\,\cdot\,\mathbf{invoer}=0$ en veranderen de gewichten niet.<

Bekijk nu de situatie fout= -2. Dan is de gewenste voorspelling voor een punt $[1,x,y]$ gelijk aan -1 en de voorspelling van de perceptron voor dit punt gelijk aan 1. De voorspelling kregen we van de perceptron uit de som:
$\mathbf{som}=w_{0}+w_{1}x+w_{2}y$.
Deze is in dit geval positief $(\gt 0)$. Om de som negatief $(\lt 0)$ te laten worden, ofwel de gewenste voorspelling te kunnen bereiken, moet de som in de volgende stap, dus met de nieuwe gewichten op zijn minst kleiner worden voordat som = 0 gepasseerd kan worden. De nieuwe gewichten bij fout = -2 zijn:

$[ w_{0}-2 \cdot \mathrm{leersnelheid}\,,\,w_{1}-2\cdot\mathrm{leersnelheid} \cdot x\,,\,w_{2}-2 \cdot\mathrm{leersnelheid} \cdot y]$.

De nieuwe som is dan:

$\mathrm{som}=w_{0}-2 \cdot \mathrm{leersnelheid}+(w_{1}-2\cdot\mathrm{leersnelheid} \cdot x)x+(w_{2}-2*\mathrm{leersnelheid} \cdot y)y $

Werken we de haakjes weg dan krijgen we iets mooiers:

$\mathrm{som}=w_{0}+w_{1}x+w_{2}y-2\cdot\mathrm{leersnelheid}-2\cdot\mathrm{leersnelheid} \cdot x^{2}-2\cdot\mathrm{leersnelheid} \cdot y^{2}$

En nog iets mooiers als we de leersnelheid buiten haakjes halen:

$\mathrm{som}=w_{0}+w_{1}x+w_{2}y-2\cdot\mathrm{leersnelheid}\cdot(1+ x^{2}+ y^{2})$

De oude som was $\mathrm{som}=w_{0}+w_{1}x+w_{2}y$, ofwel het eerste deel van de nieuwe som en die was groter dan nul. Omdat de leersnelheid positief is en ook $1+ x^{2}+ y^{2}$ positief is, wordt dus een positief getal $2 \cdot \mathrm{leersnelheid} \cdot (1+ x^{2}+ y^{2})$ van iets positiefs afgetrokken. De nieuwe som is dus echt kleiner. De regel voor de verandering van de gewichten werkt dus in ieder geval voor fout= -2.

Opdracht

Laat zelf met een vergelijkbare redenering zien dat ook voor fout=2 de regel werkt. antwoord
Zelf doen!

Figuur 7: Training perceptron met de lijn y=2x-1 ofwel 1-2x+1y=0.

Aan de slag met trainen

Voor de wiskundige onderbouwing hebben we de manier van trainen overdacht. In dit deel bekijken we deze overdenkingen met een simpele trainer alleen geschikt voor de perceptron. Deze trainer is aanwezig in de applet in figuur 7. In de applet trainen we onze perceptron met de bedoeling een juiste voorspelling voor de lijn (rood gestippeld in de figuur) $y=2x-1 \Leftrightarrow 1 - 2x + y =0$ te bereiken.

De gestreepte blauwe lijn is de representatie van de perceptron. Het doel van de trainer is dus dat de blauwe lijn op de rode lijn komt te liggen. De trainer zelf weet echter niets van de ligging van de rode lijn, behalve dat het een rechte lijn moet zijn.

De invoer (punten $(x,y)$) wordt bij toeval gekozen en de gewenste uitvoer wordt precies bepaald door de ligging ten opzichte van de lijn. Ofwel er zijn geen meetfouten in de trainingsdata. De trainer kan alleen leren van de aangeboden punten.

Uitleg applet

De knop herlaad zorgt ervoor dat er een nieuwe startwaarde voor de gewichten van de perceptron worden gemaakt.

De knop Één keer onder het kopje Per punt één training genereert één punt met bijbehorende uitvoer en past bij een fout in de voorspelling van de perceptron de gewichten aan. Druk je meerdere keren op deze knop dan gaat de training van de perceptron verder met iedere keer een nieuw punt.

Hier vind je een html bladzijde met de javascript code van de trainer alleen nog voorzien van de code voor deze optie. De graphics zijn niet aanwezig.

<html>
  <head>
    <script>
      const volgproces=false; // variabele wordt straks gebruikt om naar het console te schrijven
      var trainer=null; // de trainer van de perceptron
      /*
       De functie init maakt de trainer
      */
      function init()
      {
        trainer = new Trainer(3, Math.sign, 0.01);
      }

      // Definitie class Perceptron
      class Perceptron
      {
        /*
         * de methode constructor wordt aangeroepen als we straks
         * een Perceptron maken.
         * @param: n is het aantal inputs (inclusief de bias) die de perceptron krijgt
         * @param: f is de activeringsfunctie
         * @param: c is de snelheid van het leerproces
         */
        constructor(n,f,c) 
        {
          // Overal waar "this." voorstaat is een eigenschap
          // van een Perceptron object.
          // Wijs het aantal knopen aan 
          this.aantalInvoerKnopen = n;
          // Zet de leersnelheid 
          this.leersnelheid = c;
          // Zet de activeringsfunctie 
          this.activeringsfunctie = f;
          
          // We maken nu een eerste gok voor de gewichten voor de Perceptron
          this.gewichten=[];
          // maak random gewichten voor het perceptron  
          for(var i=0;i<n;i++)
          {
            // Trek een toevalsgetal tussen 0 en 1. Door deze
            // met 2 te vermenigvuldigen en er 1 van af
            // te trekken wordt het dus een toevals getal tussen -1 en 1
            this.gewichten[i]=2*Math.random()-1; 
          }
        }
        /*
         * geefDoor is de feed-forward functie. De invoer [1,x1,...,xn]
         * wordt verwerkt tot de uitvoer
         * @param invoer: [1,,x1,...,xn]. De 1 is er voor de bias
         */
        geefDoor(invoer)
        {
          var som =0;
          var i,uitvoer;
          // bepaal de som van de gewogen invoer
          for(i=0;i<this.aantalInvoerKnopen;i++)
          {
            som += invoer[i] * this.gewichten[i];
          }
          
          if(volgproces) console.log("De som van de gewogen invoer is "+ som);
          
          // verwerk de som met de activeringsfunctie
          return uitvoer = this.activeringsfunctie(som);
        }
        
        /* train is de functie die de gewichten aanpast bij 
         * één invoer.
         * @param invoer: de waarden van de invoer knopen 
         * vooraf gegaan door de bias=x0=1
         * dus invoer = [1, x1,x2,...]
         * @param gewensteUitvoer: wat zou de output van de percptron moeten zijn.
         */
        train(invoer,gewensteUitvoer)
        {
          var voorspelling=this.geefDoor(invoer); // Dit geeft de perceptron als voorspelling
          var fout = gewensteUitvoer - voorspelling; 
          // Pas alle gewichten aan
          for (var i = 0; i < this.aantalInvoerKnopen; i++) 
          {
            this.gewichten[i] += this.leersnelheid * fout * invoer[i];
          }
          if(volgproces) console.log("De nieuwe gewichten zijn "+ this.gewichten);
        }
        
        /* 
         * schaalPerceptron schaalt w0 terug naar 1
         * Dit is handig voor de weergave van de lijn.
         */
        schaalPerceptron()
        {
          var lijngewichten=[1];
          var w0 = this.gewichten[0];
          for(var i=1;i<this.aantalInvoerKnopen;i++)
          {
            lijngewichten[i] = this.gewichten[i]/w0;
          }
          return lijngewichten;
        }
      }

      //einde definitie Perceptron

      // begin definitie van de trainer class 

      /* 
        De finitie van de class trainer die
        wordt ingezet om een perceptron te trainen
       */
      class Trainer
      {
        /* @param: n is het aantal inputs (inclusief de bias) die de   perceptron krijgt
        * @param: c is de snelheid van het leerproces
        * @param: f is de activeringsfunctie
        */
        constructor(n,f,c) {
          this.settings={
            myPreceptron:null
          };
          this.setPerceptron(n,f,c)
        }
        
        setPerceptron(n,f,c)
        {
          this.settings.myPerceptron = new Perceptron(n,f,c);
        }
        
        /*
         * functie  eenTraining(a,b) voert één training stap uit. In de functie wordt
         *     eerst een nieuw punt gemaakt in het vierkant met zijden 8 en middelpunt
         *    (0,0). Met dat punt doet de perceptron een training.
         *    Resultaten worden in het uitvoer object getoond.
         * $param a: richtingscoëfficient in y=ax+b 
         * $param b: y-coördinaat snijpunt y-as in y=ax+b 
         */
        eenTraining(a,b)
        {
          // wat kortere benamingen
          var myPerceptron=this.settings.myPerceptron;
          
          // Maak een punt met toevalsgetallen
          var x = 8*Math.random()-4;
          var y = 8*Math.random()-4;
          // bepaal afwijking voor deze x en y t.o.v. lijn y=ax+b
          var som = -b - a*x + y;
          // maak de invoer met bias
          // bepaal gewenste voorspelling
          var gewenst=myPerceptron.activeringsfunctie(som);
          // bepaal de som met de juiste punten
          var invoer=[1,x,y];
          // bepaal de voorspelling van het perceptron
          var tekstGewichtenVoor = arrayToString(myPerceptron.gewichten,3);
          var voorspelling = myPerceptron.geefDoor(invoer);
          // train de perceptron
          myPerceptron.train(invoer,gewenst);
          // status na de training
          var tekstGewichtenNa = arrayToString(myPerceptron.gewichten,3);
          var voorspellingNaTraining = myPerceptron.geefDoor(invoer);
          
          // produceer tekst voor de gebruiker over de huidige toestand
          var tekst="Gewenste voorspelling voor<br/>"+
            "punt [" + arrayToString(invoer,2) + "] is " + gewenst +
            "<br/> bij de lijn y="+a+"x + "+b+"."+
            "<br/>Voorspelling voor training is " + voorspelling + 
            ".<br/>Gewichten:<br/>"+
            "voor training: [" + tekstGewichtenVoor+"]."+
            ".<br/>na training: [" + tekstGewichtenNa +"]." +
            ".<br/>De voorspelling na training: " + voorspellingNaTraining;
            
          if(voorspelling==gewenst)
          {
            tekst+=".<br/>Gewenst en voorspelling zijn gelijk dus er is niets gebeurd";
          }
          else
          {
            tekst+=".<br/>Gewenst en voorspelling zijn niet gelijk dus de gewichten zijn veranderd";
          
          }
          // plaats de tekst in het uitvoerveld
          document.getElementById("uitvoer").innerHTML=tekst;
      
        }
      }

      //einde trainer
      
      // andere functies

      /* de functie yLine berekent de y waarde bij gegeven x voor
         de lijn y=ax+b
      */
      function yLine(a,b,x)
      {
        return a*x+b;
      }
      
      /*
       * functie vraagt aan de perceptron in welk gebied het punt ligt
       * @param punt: [1, x-coördinaat , y - coördinaat ]
       */
      function waarLigtPunt(punt)
      {
        var invoer = eval(document.getElementById(punt).value)
        if(trainer==null) trainer = new Trainer( invoer.length, Math.sign, 0.01 );
        document.getElementById("uitvoer").innerHTML=
          "De output voor het punt " + invoer + " is " + trainer.settings.myPerceptron.geefDoor(invoer);
      }
      
      /*
       * functie arrayToString maakt van een getallen rij een
       * komma gescheiden reeks in hetgewenste aantal decimalen
       * @param array: de javascript array
       * @param decimals: het gewenste aantal decimalen
       */
      function arrayToString(array,decimals)
      {
        var tekst="";
        var first=true;
        for(var i=0;i<array.length;i++)
        {
          if(first) first=false;
          else tekst+=",";
          tekst+=array[i].toFixed(decimals);
        }
        return tekst;
      }
      
    </script> 
    </head>
    <body onload="init()" style="margin:0px; ">
    <!--<p><b>Trainen met de lijn<br/>y=2x-1 ofwel 1-2x+1y=0</b></p>
    Train de perceptron met een willekeurig
    gekozen punt<br/>-->
    Één training:<br/>
    <button class="knop" onclick="location.reload();">Herlaad</button>
    <button class="knop" onclick="trainer.eenTraining(2,-1)">Één keer</button>
    <p id="uitvoer" style="font-size: smaller; overflow-y: auto; width: 250px; height: 170px;"></p>
    </body>
</html>

De knop 100 keer onder het kopje Per punt één training genereert 100 punten met bijbehorende uitvoer en past bij een fout in de voorspelling van de perceptron de gewichten aan. Druk je meerdere keren op deze knop dan gaat de training van de perceptron verder met iedere keer een toevoeging van 100 punten. De oude punten doen niet meer mee in de training.

Voor deze situatie is aan de trainer class hierboven de functie nTraining(a,b) toegevoegd.

/*
 * functie  nTraining(a,b) voert één training stap per punt uit. In de functie wordt
 *     n keer een nieuw punt gemaakt in het vierkant met zijden 8 en middelpunt
 *    (0,0). Met dat punt doet de perceptron één training.
 *    Resultaten worden in het uitvoer object getoond.
 * $param a: richtingscoëfficient in y=ax+b 
 * $param b: y-coördinaat snijpunt y-as in y=ax+b 
 */
nTraining(a,b,n=100)
{
  var myPerceptron=this.settings.myPerceptron;
  var i,k=0,gewenst,voorspelling;
  var x,y,som,invoer,tekst="";
  for(i=0;i<n;i++)
  {
	// Maak een punt met toevalsgetallen
	x = 8*Math.random()-4;
	y = 8*Math.random()-4;
	som = -b - a*x + y;
	// maak de invoer met bias
	// bepaal gewenste voorspelling
	gewenst=myPerceptron.activeringsfunctie(som);
	// bepaal de som met de juiste punten
	invoer=[1,x,y];
	// bepaal de voorspelling van het perceptron
	voorspelling = myPerceptron.geefDoor(invoer);
	if(gewenst!=voorspelling)
	{
	  // voer een perceptron training uit
	  myPerceptron.train(invoer,gewenst);
	  // produceer tekst voor de gebruiker over de nieuwe toestand
	  k++;
	  tekst+=
		"Nieuwe gewichten bij punt "+i+" : [" + 
		arrayToString(myPerceptron.gewichten,3) +"]<br/>";      
	}
  }
  // geen aanpassingen gewichten geweest
  if( k==0 )
  {
	tekst = "Gewichten blijven : [" + 
	  arrayToString(myPerceptron.gewichten,3) +"]<br/>";  
  }
  // plaats de tekst in het uitvoerveld
  var gewichtenGeschaald = myPerceptron.schaalPerceptron();
  document.getElementById("uitvoer").innerHTML="Er "+(k!=1?"zijn "+k+" punten":" is één punt")+
	  " effectief geweest.<br/>"+
	  "Gevonden vergelijking van de lijn is nu<br/>0 = 1 + " +
	  gewichtenGeschaald[1].toFixed(3) + "x + " + 
	  gewichtenGeschaald[2].toFixed(3) +
	  "y<br/>>Als benadering voor de lijn<br/>0="+(-b)+"+"
	  + (-a)+"x + y<br/>"+tekst ;
}

De knop Één keer onder het kopje Tot goede voorspelling -per punt genereert één punt met bijbehorende uitvoer en past bij een fout in de voorspelling van de perceptron de gewichten aan net zolang tot het punt door de perceptron goed wordt voorspeld.

Voor deze situatie is aan de trainer class hierboven de functie eenTrainingTotKlopt(a,b) toegevoegd.

/*
 * functie eenTrainingTotKlopt(a,b) voert meerdere trainingen met het zelfde uit, 
 *    tot dat het punt goed wordt voorspeld.
 *    In de functie wordt  eerst een nieuw punt gemaakt in het vierkant met zijden 8 
 *    en middelpunt (0,0). Met dat punt doet de perceptron een training.
 *    Resultaten worden in het uitvoer object getoond evenals de lijnenwaaier van
 *    de tussenstappen.
 * $param a: richtingscoëfficient in y=ax+b 
 * $param b: y-coördinaat snijpunt y-as in y=ax+b 
 */
eenTrainingTotKlopt(a,b)
{
  var myPerceptron=this.settings.myPerceptron;
  var tekst,x,y,invoer,gewenst,uitgevoerd,som,i=1;
  x = 8*Math.random()-4;
  y = 8*Math.random()-4;
  som = -b - a*x + y;
  invoer=[1,x,y];
  gewenst=myPerceptron.activeringsfunctie(som);
  tekst="Stap 0: Begingewichten: [" + arrayToString(myPerceptron.gewichten,3) +"]<br/>";
  tekst+="Trainings punt ["+arrayToString(invoer,2)  + "]<br/>met gewenste uitvoer: "+gewenst+ "<br/><br/>";
    
  do
  {
    tekst+="Stap "+i+":Voorspelling:<br/>";
    tekst+="voor training "+myPerceptron.geefDoor(invoer) +"<br/>";
    myPerceptron.train(invoer,gewenst);
    tekst+="na training "+myPerceptron.geefDoor(invoer) +"<br/>";
    tekst+=
      "Nieuwe gewichten: [" + arrayToString(myPerceptron.gewichten,3) +"]<br/><br/>";
    uitgevoerd=myPerceptron.geefDoor(invoer);
    i++;
  }
  while(uitgevoerd!=gewenst)
  var gewichtenGeschaald = myPerceptron.schaalPerceptron();
  document.getElementById("uitvoer").innerHTML =
    "Aantal aanpassingen: "+ i+
    "<br/>Gevonden vergelijking van de lijn is<br/>0 = 1 + " +
    gewichtenGeschaald[1].toFixed(3) + "x + " + 
    gewichtenGeschaald[2].toFixed(3) +
    "y<br/>Als benadering voor de lijn<br/>0="
    +(-b)+"+" + (-a)+"x + y<br/><br/>"+tekst;
}

De knop 100 keer onder het kopje Tot goede voorspelling -per punt genereert 100 punten met bijbehorende uitvoer en past voor ieder opvolgend punt bij een fout in de voorspelling van de perceptron de gewichten aan net zolang tot dit punt door de perceptron goed wordt voorspeld.

Voor deze situatie is aan de trainer class hierboven de functie nTrainingTotKlopt(a,b) toegevoegd.

/* functie nTrainingTotKlopt(a,b) voert 100 keer
 *    meerdere trainingen met een zelfde punt uit, 
 *     tot dat het punt goed wordt voorspeld.
 *    In de functie wordt  100 keer 
 *    eerst een nieuw punt gemaakt in het vierkant met zijden 8 
 *    en middelpunt (0,0). Met dat punt doet de perceptron een training.
 *    Het laatste resultaat wordt in het uitvoer object getoond.
 * $param a: richtingscoëfficient in y=ax+b 
 * $param b: y-coördinaat snijpunt y-as in y=ax+b 
 */
nTrainingTotKlopt(a,b,n=100)
{
  var myPerceptron=this.settings.myPerceptron;
  var x,y,invoer,som,i=1,j,k=0;
  var gewenst,voorspeld
  var tekst="";
  for(j=0;j<n;j++)
  {
    x = 8*Math.random()-4;
    y = 8*Math.random()-4;
    som = -b - a*x + y;
    invoer=[1,x,y];
    i=0;
    gewenst=myPerceptron.activeringsfunctie(som);
    while(gewenst!=(voorspeld=myPerceptron.geefDoor(invoer)))
    {
      myPerceptron.train(invoer,gewenst);
      i++;
    }
    if(i>0)
    {
      k++;
      tekst+=
        "Nieuwe gewichten bij punt "+j+" in "+i+(i>1?" stappen":" stap")+": [" + 
        arrayToString(myPerceptron.gewichten,3) +"]<br/>";
    }
  }
  // geen aanpassingen gewichten geweest
  if( k==0 )
  {
    tekst = "Gewichten blijven : [" + 
      arrayToString(myPerceptron.gewichten,3) +"]<br/>";  
  }        
  var gewichtenGeschaald = myPerceptron.schaalPerceptron();
  document.getElementById("uitvoer").innerHTML = 
    "<br/>Gevonden vergelijking van de lijn is<br/>0 = 1 + " +
    gewichtenGeschaald[1].toFixed(3) + "x + " + 
    gewichtenGeschaald[2].toFixed(3) +
    "y<br/>Als benadering voor de lijn<br/>0="
    +(-b)+"+" + (-a)+"x + y<br/><br/>"+tekst;
}

De knop voeg 25 punten toe onder het kopje Per verzameling genereert 25 punten met bijbehorende uitvoer en voegt die toe aan trainingsdata. Vervolgens wordt de strategie 1 punt per training toegepast op de trainingsdata en eventueel herhaald tot er geen verandering meer is van de gewichten.

Voor deze situatie is aan de trainer class hierboven de functie sampleTrainingTotKlopt(a,b) toegevoegd.

/*
 * functie sampleTrainingTotKlopt(a,b,n) voert 
 *    meerdere trainingen op een punten verzameling uit, 
 *     tot dat de verzameling goed wordt voorspeld.
 *    In de functie wordt  n keer 
 *    eerst een nieuw punt gemaakt in het vierkant met zijden 8
 *    en middelpunt (0,0)  en toegevoegd aan de puntenverzameling. 
 *     Met de punten in de verzameling doet de perceptron een training.
 *    De verzameling wordt net zolang aangeboden
 *    tot alle punten goed worden voorspeld
 * $param a: richtingscoëfficient in y=ax+b 
 * $param b: y-coördinaat snijpunt y-as in y=ax+b 
 * $param n: punten die aan de verzameling moeten worden toegevoegd       
 */
sampleTrainingTotKlopt(a,b,n = 25)
{
  var myPerceptron=this.settings.myPerceptron;
  var puntenVerzameling = this.settings.puntenVerzameling;
  var i,x,y,som,invoer,gewenst;
  var veranderd = 0;
  var ronde = 0;
  var tekst = "";
  var vl = puntenVerzameling.length;
  // voeg punten toe
  var eind = vl+n;
  for(i=vl;i<eind;i++)
  {
	  x = 8*Math.random()-4;
	  y = 8*Math.random()-4;
	  som = -b - a*x + y;
	  invoer=[1,x,y];
	  gewenst=myPerceptron.activeringsfunctie(som);
	  puntenVerzameling[i]=[invoer,gewenst];
  }
  // herhaal training tot er geen foute plaatsing meer is
  do
  {
	  veranderd = 0;
	  // ga alle punten af (we gaan van eind naar begin 
	  // om eerst de toegevoegde punten te behandelen)
	  for(i=eind-1;i>=0;i--)
	  {
	    if(puntenVerzameling[i][1]!=myPerceptron.geefDoor(puntenVerzameling[i][0]))
	    {
		    myPerceptron.train(puntenVerzameling[i][0],puntenVerzameling[i][1]);
		    veranderd++;
	    }
	  }
	  ronde++;
	  tekst += "Ronde "+ronde + ":Aantal veranderingen: "+veranderd +"<br/>"+
			"Perceptron gewichten: ["+arrayToString(myPerceptron.gewichten,3)+"]<br/>";
  }
  while (veranderd!=0)
  var gewichtenGeschaald = myPerceptron.schaalPerceptron();
  document.getElementById("uitvoer").innerHTML = 
	"Aantal rondes:"+ronde+
	"<br/>Gevonden vergelijking van de lijn is<br/>0 = 1 + " +
	gewichtenGeschaald[1].toFixed(3) + "x + " + 
	gewichtenGeschaald[2].toFixed(3) +
	"y<br/>Als benadering voor de lijn<br/>0="
	+(-b)+"+" + (-a)+"x + y<br/><br/>"+tekst;
}

Onderzoeksvragen

Druk bij per punt één training herhaaldelijk op de knop Één keer. In welke gebieden wordt de perceptron aangepast en in welke gebieden niet?
antwoord

Er vindt alleen een verandering van de perceptron plaats als de voorspelling van de perceptron bij een punt niet gelijk is aan de gewenste voorspelling. Je ziet waarschijnlijk ook dat het punt dan in een gebied tussen de twee lijnen ligt.
Druk bij per punt tot goede voorspelling herhaaldelijk op de knop Één keer. Soms zie je bij de doorgaande training dat er een lijnenwaaier getoond wordt. Waarom?
antwoord

Er komt een lijnenwaaier als er per punt meerdere keren getraind wordt. Merk ook op dat de lijn voorstelling van de perceptron draait naar de werkelijk lijn, al kan dat wel een draaiing zijn van meer dan 90 graden. De oorzaak van een grote draaiing is het teken van de gewichten. Waarom? Wel als je $a+b⋅x+c⋅y=0$ vergelijkt met $−a−b⋅x−c⋅y=0$ dan zijn beide een vergelijking voor de zelfde lijn, echter het teken bij een willekeurig punt niet op de lijn is tegenovergesteld. De lijn wijst als het ware de andere kant op.
Druk op herlaad en druk daarna bij per punt één training op de knop 100 keer. Hoe vaak vond er een verandering van de gewichten plaats? (Herhaal dit een aantal malen)
antwoord

Je observeert dat veel minder dan 50% van de punten geen verandering geven. Je schiet dus vaak mis bij het sturen van het netwerk. Dit is één van de redenen dat het trainen van een Neuraal Netwerk zo lastig.
Je ziet waarschijnlijk een flink aantal punten die tussen de twee lijnen liggen. Wat zouden die punten nog kunnen betekenen in een vervolg van het trainingsproces?
antwoord

Afhankelijk van het toeval valt na 100 keer de blauwe lijn meer of minder samen met de groene. De punten tussen de lijnen geven nog een foute voorspelling en zouden dus nogmaals gebruikt kunnen worden in het trainingsproces.
Druk op herlaad en druk daarna bij per punt tot goede voorspelling op de knop 100 keer. Hoe vaak vond er een verandering van de gewichten plaats?(Herhaal dit een aantal malen)
antwoord

Je observeert dat nog steeds veel minder dan 50% van de punten een verandering geven. Je ziet ook dat er nu punten zijn waarvoor er meer stappen per punt worden gemaakt om dat punt goed te laten voorspellen.
Ook hier zie je ook nog punten tussen de lijnen liggen. Waarom? Wat zouden die punten nog kunnen betekenen in een vervolg van het trainingsproces?
antwoord

Ondanks dat we ieder punt het netwerk trainen totdat het punt goed voorspeld wordt, blijft deze eigenschap niet noodzakelijk aanwezig in een volgende training van een ander punt. De gewichten kunnen dan zo worden aangepast dat de lijn bepaald door die gewichten net een andere draaiing krijgt. Het resultaat kan dan zijn dat een eerder goed voorspeld punt aan de verkeerde kant van de lijn behorend bij de gewichten komt te liggen. De punten tussen de lijnen geven nog een foute voorspelling en zouden dus nogmaals gebruikt kunnen worden in het trainingsproces.
Druk op herlaad en druk daarna bij per verzameling tot goede voorspelling op de knop voeg 25 punten toe. Hoe veel rondes worden uitgevoerd en hoe vaak vond er in totaal een verandering van de gewichten plaats?(Herhaal dit een aantal malen)
antwoord

Je observeert dat er meestal meerdere trainingsrondes over de verzameling worden uitgevoerd, waar meer of minder trainingen moeten worden gedaan. Deze vorm van trainen wordt het meest gebruikt bij het trainen van een netwerk. Een verzameling van punten wordt meerdere malen aan het netwerk aangeboden. Daarbij kan er, als er foutieve invoer/uitvoer aanwezig is, wel sprake zijn van wat men noemt een overtraining van een netwerk. Dat wil zeggen dat de foutieve waarden een grotere invloed hebben op de voorspellingen.
Hier zie je geen punten meer tussen de lijnen liggen. Waarom?
antwoord

Er wordt net zolang getraind tot alle punten juist worden voorspeld. Alleen tussen de lijnen is er een verschil in het teken en daar liggen de punten die niet juist worden voorspeld. Die zijn er niet meer.
Soms zie je dat het aantal aanpassingen in een volgende ronde hoger is. Waarom?
antwoord

In de voorgaande opdrachten heb je gezien dat een lijn weg kan draaien van al eerder juist voorspelde punten. Dit draaien kan er soms voor zorgen dat er meerdere punten in de verkeerde zone komen te liggen.

Discussie

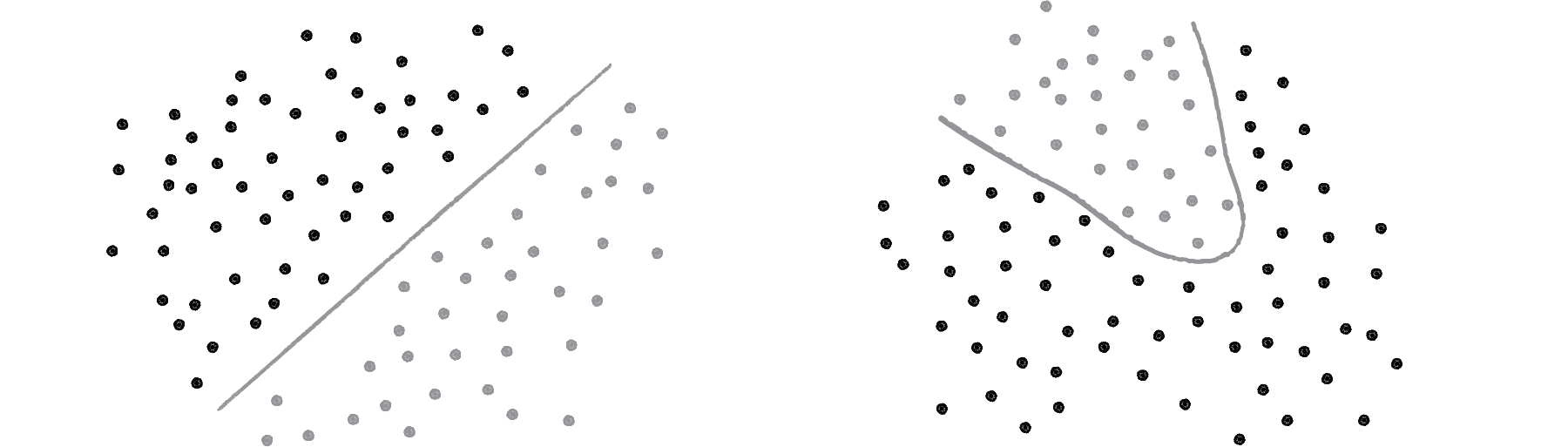
figuur 8: Het probleem links kan wel met één perceptron worden opgelost, er is één grenslijn. Het probleem rechts kan niet met één perceptron worden opgelost, de grens is niet lineair. Bron:Nature of code

In het laatste stuk van dit hoofdstuk vatten we de mogelijkheden, onmogelijkheden en eigenschappen van de perceptron, het simpelste neurale netwerk, samen. Als eerste moet je beseffen dat een enkele perceptron ( en dus ook iedere knoop in een ingewikkelder neuraal netwerk) slechts één lineair probleem kan oplossen (zie figuur 8).
Een lineair probleem is daarin niet alleen een lijn. Met bijvoorbeeld drie invoeren en de bias heeft het preceptron 4 gewichten die samen de vergelijking $w_{0} + w_{1} \cdot x + w_{2} \cdot y + w_{3} \cdot z = 0$ als grens vormen. Dit is de vergelijking van een plat vlak. In de wiskunde staat lineair voor termen waarin er geen machten, producten of andere functies van termen staan. Zo zijn bijvoorbeeld $1 + x^2 + y = 0$ , $2 + x \cdot y + 3 y = 0$ en $1 + log(x) + \sin(y) = 0$ geen lineaire vergelijkingen.

Neurale netwerken zijn te trainen om o.a. handschriften, geluiden en te gezichten te herkennen. Dit zijn zeker geen lineaire structuren. Gelukkig kun je dit soort structuren weer opknippen in lijnstukjes of platte figuurtjes die dan wel weer door één preceptron te leren zijn. Er moeten dan natuurlijk wel meerdere perceptrons in het netwerk aanwezig zijn. Hoe complex zo'n netwerk moet zijn is niet altijd makkelijk te bepalen. In het volgende hoofdstuk gaan we hier dieper op in. Op de afbeelding hieronder, die je ook al gezien in het hoofdstuk technieken, zie je dat er heel veel typen neurale netwerken zijn. Ieder type heeft een eigen toepassingsgebied. Klik hier of op de afbeelding als je er meer over wilt weten.

In het trainen van ons simpele netwerk heb je al gezien dat er heel veel trainingspunten nodig zijn. Dit is in het algemeen zo. Het leren van een netwerk kost veel tijd en energie. In ons simpele netwerk waren er slechts drie gewichten die moeten worden aangepast. Zetten we er nog een zelfde perceptron naast dan worden dat er al zes. In een netwerk van zes knopen met twee inputs en een bias zijn dat er al $6 \cdot 3 = 18$. Om al die gewichten voldoende nauwkeurig te schatten zijn heel veel datapunten nodig.

Kunstmatige Intelligentie/Neurale Netwerken/Hoe een neuraal netwerk leert

Bronnen:Nature of code, hoofdstuk 10 , Learn Neural Networks with Brain.js by Robert Plummer , brains.js