Op weg naar meer lagen

Kunstmatige Intelligentie/ Neurale Netwerken/Op weg naar meer lagen

Creative Commons License
This work is licensed under a
Creative Commons Attribution-NonCommercial-ShareAlike 4.0
International License.
Inleiding Logische schakelingen Bias Lijnen Bias vervolgd Lijnen vervolgd Quickdraw vervolgd

Inleiding



figuur 1: Een fouten landschap en het pad naar de kleinste fout met een gradiënt techniek. Volg de steilste helling vanaf het startpunt. Verschillende startpunten kunnen een ander minimum opleveren.

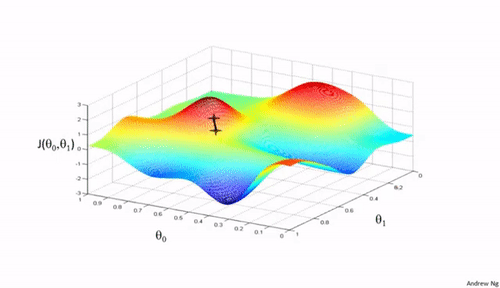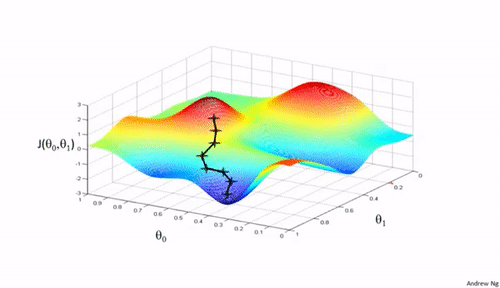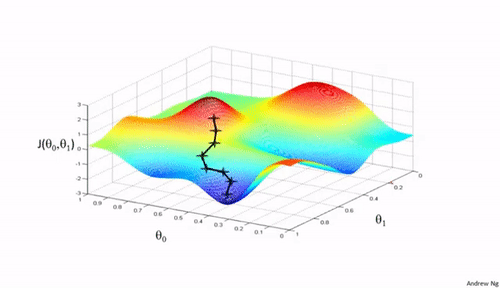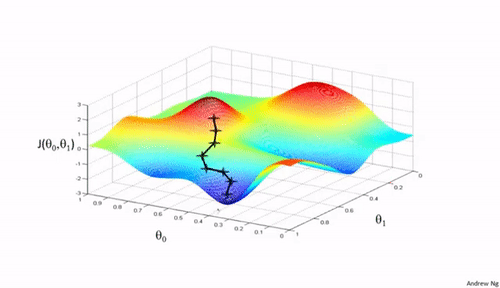
In het hoofdstuk technieken zijn al verschillende netwerken gepresenteerd en welke leerstrategieën er zijn. Ook hebben we in de vorige paragraaf het kleinste netwerk, de preceptron, in meer detail bekeken en deze via begeleid leren getraind tot een zo klein mogelijke fout in de voorspelling. Je hebt daar gezien dat de gewichten van de enige perceptron in dit netwerk zich ook bewijsbaar laat aanpassen aan de trainingsdata, door in te spelen op de grootte van de fout. De gebruikte trainingsmethode valt onder wat men noemt de gradiënt technieken.


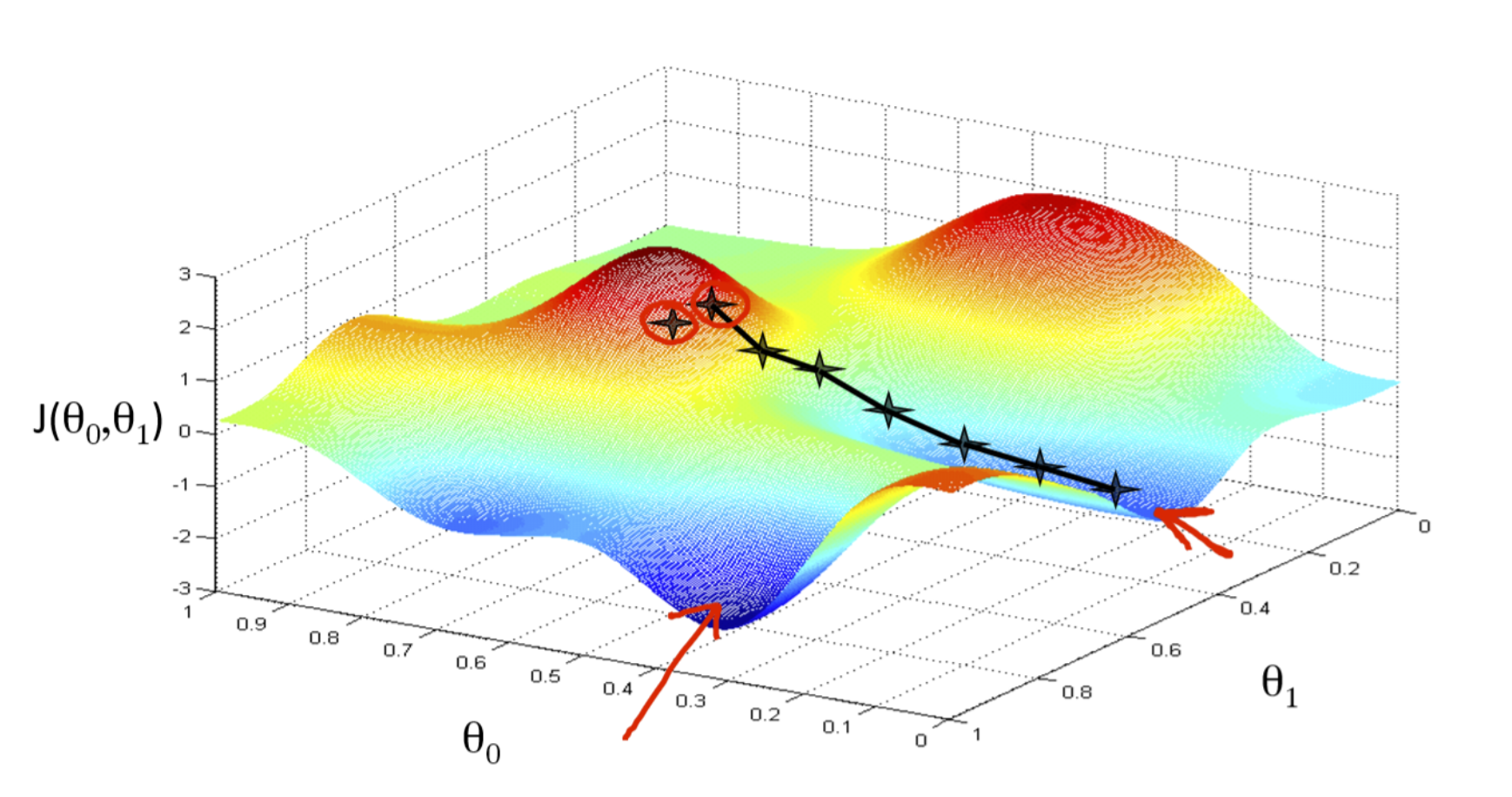
Bij een gradiënt techniek wordt in een toestand bepaald in welke richting de toestand het snelst kan veranderen in de richting van een gewenste toestand. In de wiskunde wordt snelheid in een punt (=toestand) bepaald door de waarde van de afgeleide (=helling = gradiënt) in dat punt. In het trainen van neurale netwerken is de gewenste toestand het punt waar de fout zo klein mogelijk is. In figuur 1 zie je een hypothetisch voorbeeld. Bij een gegeven set trainingsdata zie je een berglandschap met op de z-as de grootte van de fout bij bepaalde waarden van de gewichten (de twee andere assen, dus hier gaat het slechts om twee gewichten). Bij het leren start je ergens in dit landschap en volg je het steilste pad naar een laag punt in het landschap. De zwarte lijntjes zijn voorbeelden van zulke paden in dit landschap. Je ziet dat je niet altijd op de juiste of wel de laagste plek in het landschap terecht komt. Het startpunt en de vorm van het landschap bepaalt waar je uiteindelijk terecht komt. Er wordt dan ook vaak meerdere keren vanuit andere startpunten geleerd. In de meeste neurale netwerken zijn er veel knopen en meerdere lagen, dus ook veel meer gewichten (is meer assen en dus nog meer dimensies) die aangepast moeten worden. Het foutenlandschap kan dan nog ingewikkelder worden.

Als er meerdere verborgen lagen in het netwerk aanwezig zijn, in de meeste gevallen dus, is het idee van trainen hetzelfde als bij het netwerk bestaande uit één perceptron. Het probleem is dat je de fout bij een trainingspunt alleen meet aan het eind van het netwerk. Echter ook in de tussenlaag hebben we een fout nodig om te kunnen corrigeren. De techniek om de uiteindelijke fout door het netwerk te sturen noemt men back propagation. In de onderstaande video wordt dit idee uitgelegd en in een iets bredere context geplaatst.

In deze cursus gaan we niet op de wiskunde van back propagation in, omdat, zoals je in de video kan zien, de onderliggende wiskundige technieken nog niet bij jullie bekend zijn. Voel je je echter uitgedaagd dan zijn er vele plekken met uitleg op het internet te vinden, b.v. Matt Mazur en Mikael Laine.

In dit hoofdstuk ga je onderzoeken wat het effect is van keuzes in vorm van het netwerk en de keuzes in de instellingen van het trainingsproces. Je gebruikt daarvoor een aantal applets die zijn gebouwd op de bibliotheek van brain.js. In deze applets bieden we je een aantal voorbeelden aan, maar kun je zo je wilt ook eigen trainingsdata voor een probleem invoeren. Al deze voorbeelden blijven eenvoudig. Het doel is te ervaren waar je zoal op moet letten als je een netwerk bouwt en gaat trainen.


Simpele logische schakelingen

We beginnen met het trainen van een simpel netwerk dat moet leren om te bepalen of iets waar is of niet waar, gebaseerd op een netwerk met twee inputs die elk waar of niet waar zijn. Om dit een beetje een context te geven gaan we dit voorbeeld ophangen aan de huisdieren kat en hond en kindertal. We laten het netwerk dan een uitspraak doen over jouw keuze.

De dierenliefhebber
x1∨x2=...
0∨0=0
0∨1=1
1∨0=1
1∨1=1
huisdier?status
kathond=dierenliefhebber?
neenee=nee
neeja=ja
janee=ja
jaja=ja

Een persoon kan een kat, een hond, beide of geen van beide als huisdier hebben. Heeft de persoon er minstens één, dan vinden we het een dierenliefhebber, anders niet. Zie de tabel links. Dit is een voorbeeld van de logische schakeling of ofwel de of-poort. We kunnen dit voorbeeld omzetten in getallen zodat we het de computer kunnen voeren, nee wordt 0 en ja wordt 1. Het wel of niet hebben van een kat wordt de eerste input (x1) en het wel of niet hebben van een hond wordt de tweede input (x2) van het netwerk. Een abstractere weergave van dit probleem wordt dan de tabel rechts. Deze tabel geeft alle combinaties die mogelijk voor dit probleem en daarmee gaan we ons netwerk trainen. Aan het eind van het trainen moet je dan met de invoer [1,0] de uitvoer 1 krijgen, ofwel in het bezit van een kat ben je een dierenliefhebber.

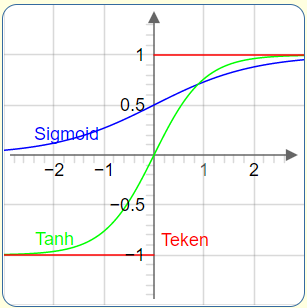
Voor dit probleem een neuraal netwerk gebruiken is echte onzin, want je kunt zonder trainen je vraag opzoeken in de tabel. Dat we het toch doen is om te leren hoe effectief het netwerk kan leren. Open deze applet en ga op onderzoek uit. De activeringsfunctie die in dit voorbeeld wordt gebruikt is de sigmoïde functie $\sigma(x)$, die waarden tussen 0 en 1 kan aannemen, echter niet de waarden 0 en 1 zelf. Hoe groter (of kleiner) $x$ hoe dichter $\sigma(x)$ bij 1 ( of 0)

Opdrachten
  1. Druk vier keer op de knop en vul de tabel in behorende bij opdracht 1 in aanwezig in dit 📎 Excel document in het tabblad "Logische schakeling or" en beantwoord de volgende vragen:
    aantal iteraties eindfout voorspelde vergelijkingen (geschaald en ongeschaald
    1. Is het aantal iteraties gelijk?
    2. Is de fout altijd gelijk?
    3. Zijn de vergelijkingen precies gelijk?
    4. Wat is hiervoor de verklaring?
      antwoord
      • Bij het begin van iedere training worden de de gewichten in de vergelijkingen bij toeval gekozen. Dit zorgt ervoor dat het pad naar de uiteindelijke oplossing niet gelijk is (zoiets als een andere startwaarde in figuur 1) en de grens die je aan de fout hebt gesteld met een net andere waarde wordt overschreden. Als je naar de geschaalde vergelijkingen kijkt zie je wel bijna dezelfde vergelijking.
  2. Waarom is het trainen zonder verborgen lagen hier mogelijk?
    antwoord
    • Je ziet in de grafische weergave dat er in de puntenwolk één lijn kan worden getekend die de rode en de blauwe punten van elkaar kan scheiden. Dit is precies de situatie die een enkele perceptron aankan. In het or netwerk is dat de knoop in de output laag.
  3. In deze opgave bekijken we het effect van de drempelwaarde in de fout (treshold). Vul de tabel bij opdracht 3 in bovenstaand Excel document en beantwoord de volgende vragen:
    threshold aantal iteraties voorspelde vergelijkingen
    (geschaald en ongeschaald)    		 voorspelling [0,0] som (on)geschaald invoer [0,0]
    0.05
    0.01
    0.005
    0.001
    0.0005
    1. Bij groter wordende fout neemt het aantal iteraties af. Welke verband zie je verschijnen, lineair, exponetiëel, omgekeerd evenredig, kwadratisch (maak een grafiek met de getallen)?
      antwoord
      • Ons resultaat:
        Maak zelf de grafiek en zie een omgekeerd evenredig (hyperbolisch) verband verschijnen, $iteraties = \frac{c}{fout}$.
        Omdat de sigmoïde functie nooit de waarde 1 kan bereiken, kan fout = 0 nooit worden gehaald en kun je ook nooit onder 0 iteraties komen.
    2. Kijk naar de geschaalde vergelijkingen ( $x_{1}+a \cdot x+{2}=b$ ) Wat valt je op?
      antwoord
      • Op de constante b na lijken de lijnen bijna gelijk.
    3. De geschaalde vergelijkingen zijn verkregen door te delen door de factor voor $x_1$ in de ongeschaalde vergelijkingen. Als je een invoer (b.v. $[x_1,x_2]=[0,0]$) aan het netwerk geeft berekent het netwerk met deze invoer de som:
      $som=a \cdot x_1+b\cdot x_2 + c$
      Vul nu de laatste twee kolommen voor invoer [0,0] in (vergeet niet bij de geschaalde vergelijkingen de constante term naar links te halen).Vul de waarden gevonden in deze kolommen in, in de functie $\sigma(som) = sigmoïde(som) = 1/(1+e^{-som})$.
      Wat valt je op als je de fout kleiner maakt?
      antwoord
      • Invullen van [0,0] in de ongeschaalde som levert precies de voorspelde waarde van het netwerk. Bij kleinere fout verandert de positie van de lijn nauwelijks. De waarden van de coëfficiënten nemen toe waardoor de som groter wordt en beweeg je verder naar de extremen van de sigmoïde functie. Dit gebeurt ook in de knopen van netwerken met meer lagen. De invoer naar opvolgende knopen zorgen voor een hoger onderscheidend vermogen van het netwerk als die invoer grotere verschillen heeft. b.v. (0,1) versus (0.45 , 0.55). Dus grotere gewichten leiden tot een groter onderscheidend vermogen..

Hotel de botel van dieren
x1∧x2=...
0∧0=0
0∧1=0
1∧0=0
1∧1=1
huisdier?status
kathond=Hotel de botel?
neenee=nee
neeja=nee
janee=nee
jaja=ja

Weer kan een persoon kan een kat, een hond, beide of geen van beide als huisdier hebben. Heeft de persoon er twee, dan is deze persoon hotel de botel ofwel stapelgek op dieren, anders niet. Zie de tabel links. Dit is een voorbeeld van de logische schakeling and ofwel de en-poort. De abstractere weergave van dit probleem wordt nu de tabel rechts. Open weer de deze applet en ga op onderzoek uit.

Opdracht
  1. Verander de trainingsdata naar de uitvoer van de en-poort gegeven in de tabel rechts:
    Wat observeer je als je het netwerk dan traint?
    antwoord
    • Je observeert dat er ook hier een lijn is die net als bij de or-poort de punten netjes verdeeld. De belangrijkste observatie is dat door alleen de trainingsdata te veranderen en niet het programma te wijzigen het netwerk ook andere situaties kan leren. Ofwel de trainingsdata bepaalt het voorspellend vermogen van het netwerk.
Verantwoordelijke voortplanting
x1⊻x2=...
0⊻0=0
0⊻1=1
1⊻0=1
1⊻1=0
kind?status
jongenmeisje=Verantwoordelijk?
neenee=nee
neeja=ja
janee=ja
jaja=nee

Op dit moment zijn er meer dan 7 miljard mensen op aarde, deze hebben niet allemaal dezelfde welvaart. Als iedereen dezelfde welvaart als de gemiddelde Nederlander zou hebben dan is, volgens sommigen, de draagkracht van de aarde 1,5 tot 2 miljard mensen. Om terug te gaan naar deze bevolkingsomvang zouden gezinnen een tijd precies hooguit één nakomeling moeten krijgen. Echter een mens wil zijn genen ook graag doorgeven naar een volgende generatie. Dus één kind per stel is dan nodig. Laten we ervan uitgaan dat we in de toekomst het geslacht van kind, een jongen of een meisje, zouden kunnen kiezen en dat we er van ieder geslacht maximaal één kunnen krijgen dan ben je als stel verantwoordelijk als je één kind krijgt. Deze situatie is in de tabel links weergegeven en in de tabel rechts omgezet naar een getalswaarde. Deze situatie noemt men de exlusieve-of poort (xor (⊻)).

Opdrachten
  1. Verander de trainingsdata naar de uitvoer van de exclusieve of-poort gegeven in de tabel rechts. Je kunt dit netwerk niet trainen met de zelfde instellingen als bij de en-poort en de of-poort. Waarom niet? Wat moet er veranderen?
    antwoord
    • Je ziet dat het niet mogelijk is om de puntenwolk met slechts één lijn te scheiden. Met één enkele perceptron kan er slechts één lijn worden gemaakt. We hebben meerdere lagen nodig om dit probleem te trainen. Laad in de applet het xor voorbeeld door op de knop xor te drukken en beantwoordt de volgende vragen.
  2. Het kan zijn dat bij het indrukken van de xor knop in het menu, de training al direct mislukt. Er is bewust een situatie gecreëerd die vaak een slecht trainingsresultaat geeft. In het Excel document in het tabblad “Logische schakeling xor” vul je onder opdracht 6 de tabel in door per situatie 50 keer op de Train knop te drukken en dan het aantal trainingen en het aantal mislukkingen te tellen.
    Beantwoord daarna de volgende vragen:
    leersnelheid aantal trainingen aantal mislukkingen
    0.9
    0.7
    0.5
    0.3 (verhoog max aantal iteraties naar 100000)
    0.1 (verhoog max aantal iteraties naar 100000)

    1. Is het aantal mislukkingen bij iedere leersnelheid gelijk?
      antwoord
      • Iedere keer dat je op de train knop drukt worden de gewichten $w_0$, $w_1$ en $w_2$ bij toeval gekozen. Sommige combinaties blijken tot een niet succesvolle training te leiden. De kans dat het misgaat blijkt in onze simulaties groter te zijn als de leersnelheid hoger is. Echter bij een leersnelheid van 0.1 vonden wij ook nog een flink aantal mislukkingen. Onze reeks van 50 trainingen leverde (0.9:13, 0.7:8, 0.5:9, 0.3:4, 0.1:5)
    2. Waarom moet je het maximaal aantal iteraties verhogen bij lagere leersnelheden?
      antwoord
      • Lagere leersnelheden zorgen voor kleinere stapjes in de ruimte van mogelijke waarden voor de gewichten. Als een bepaalde set van gewichten moet worden bereikt dan doet een mier daar langer over dan een luipaard. Maar zoals we hierboven hebben ontdekt kan een luipaard zijn doel voorbij schieten.
    3. Wat valt je op in het diagram bij een mislukte training?
      antwoord
      • Er is minstens één van de twee lijnen die niet op de juiste manier punten verdeeld.
  3. In vorige opdracht zag je dat het leren zelfs bij kleine leersnelheden niet altijd tot een succesvolle training leidde. We gaan nu onderzoeken of meer knopen in een laag daar verbetering in kan brengen. Zet de leersnelheid op 0.9. Herhaal weer de procedure als boven, maar noteer ook hoe veel lijnen in het diagram de punten onjuist verdelen, ofwel een rode en blauwe regio juist scheiden.
    lagen aantal trainingen aantal mislukkingen aantal keer dat een lijn verkeerd ligt
    [3]
    [4]
    1. Is er altijd een succesvolle training?
      antwoord
      • In onze poging met met 3 knopen [3] trad er slechts één mislukking op in de 50 trainingen. In dit geval waren er 2 lijnen die de puntenwolk niet juist verdeelden. In 20 van de trainingen deelden alle 3 de lijnen de punten wolk op een juiste manier. Bij 4 knopen trad er in 200 keer trainen geen enkele mislukking op en deelden er in slechts 5 gevallen alle lijnen de punten op een juiste manier in twee groepen.
    2. Wat zou een verklaring kunnen zijn voor het succes van meerdere knopen in de verborgen laag?
      antwoord
      • Het lijkt er op dat er minimaal twee lijnen juist moeten liggen. Met meer knopen is de kans daarop groter. Het netwerk kan een slechte set start gewichten bij één knoop blijkbaar compenseren met de andere knopen.

        Voor degenen die iets van kansrekening weten zou een benadering met de binomiale verdeling misschien inzicht kunnen geven:
        Bij 2 knopen en threshold 0.9 vonden wij 2 juiste lijnen in 37 pogingen bij 50 herhalingen ofwel P=37/50=0.74.
        Omdat P( precies 2 keer een succes,n=2) = p2 is de kans p op eén juiste lijn = $\sqrt{0.74}=0.86 $.
        Zetten we deze kans door naar meer lagen dan levert de binomiale verdeling:
        Bij 3 knopen P(minstens 2 successen, n=3,p=0.86)=0.95.
        Bij 4 knopen p(minstens 2 successen, n=4,p=0.86)=0.99.
        In 50 herhalingen verwacht je dan $50 \cdot 0.95 = 47.550⋅0.95=47.5$ successen bij 3 knopen en
        $50 \cdot 0.99 = 49.5 50⋅0.99=49.5$ successen bij 4 knopen.
    3. Hoeveel iteraties zijn er nodig bij een succesvolle training bij 2 , 3 en 4 knopen bij een leersnelheid van 0.9?
      antwoord
      • Wij observeerden in bij 3 en 4 knopen gevallen rond de 1000 iteraties.
        Bij 2 knopen waren er vaak uitschieters naar veel meer dan 1000 iteraties nodig.
    4. Welke strategie lijkt meer succes te leveren, meer knopen per laag of een lagere leersnelheid?
      antwoord
      • Meer knopen in een tussenlaag levert met een hogere leersnelheid vaker tot een succesvolle training met minder iteraties.


Bias


figuur 5: De FAST-principes

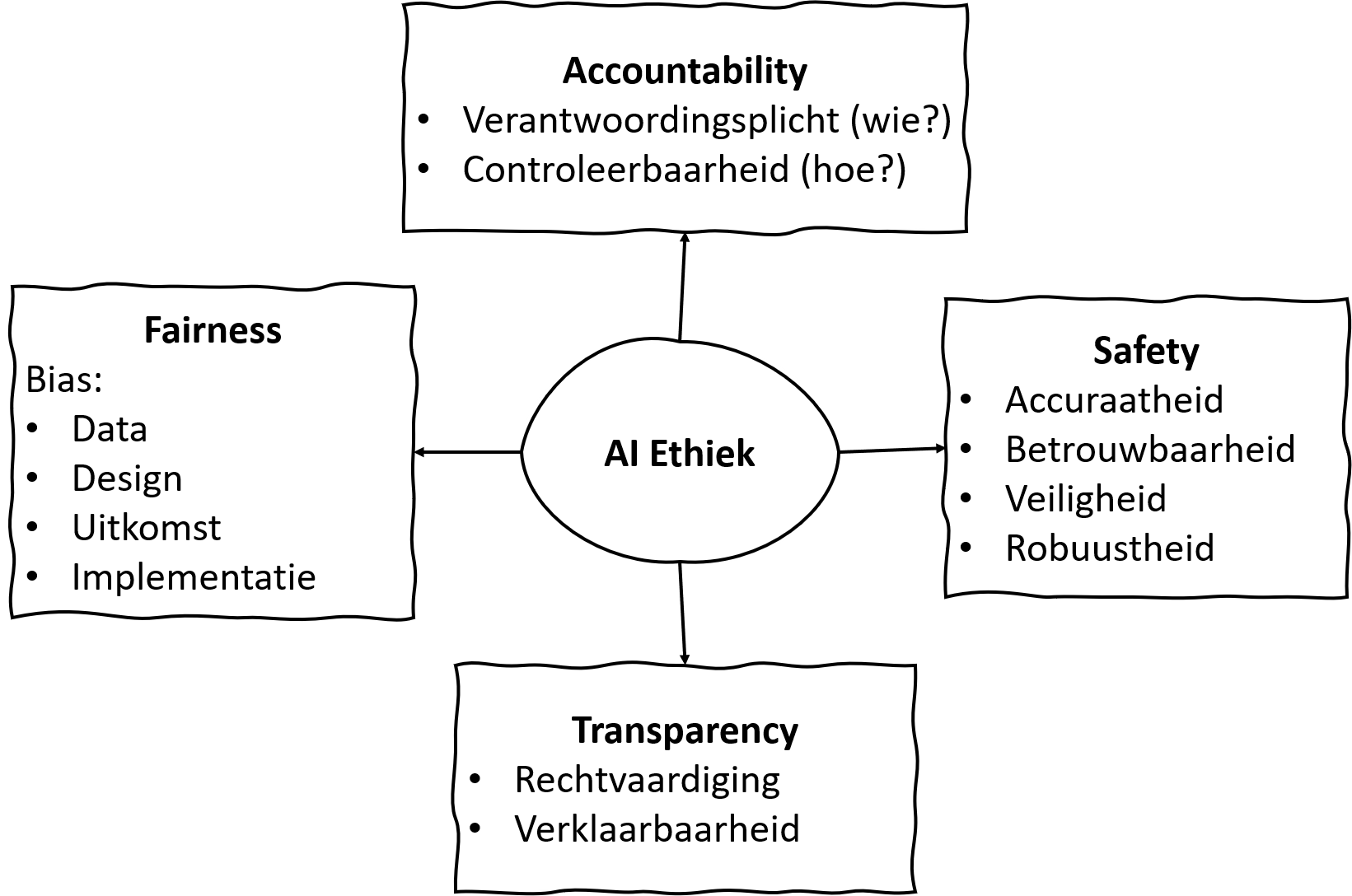
Bij het maken van een applicatie die gebruikt maakt van neurale netwerken, of AI in het algemeen, is het van groot belang aandacht te besteden aan de mogelijke problemen die deze applicatie met zich draagt. In deze cursus hebben we daarom de sectie ethiek een grote plek toebedeeld. De FAST-principes ( fairness, accountability, safety en transparency ) worden daarin uitgelegd. In dit hoofdstuk zijn we neurale netwerken aan het trainen. De opdrachten zijn er om te ontdekken hoe een netwerk te trainen is door verschillende keuzes te maken. In figuur 5 zie je onder Fairness de term bias staan en onder Transparency de termen Rechtvaardiging en Verklaarbaarheid. We beginnen met rechtvaardiging en verklaarbaarheid van een AI applicatie, gebaseerd op neurale netwerken. Om aan deze principes te kunnen voldoen moet er onder andere de volgende punten in de documentatie aanwezig zijn:

  1. de keuze in het ontwerp (design) van het netwerk
  2. de keuze in de implementatie van het netwerk
  3. de eigenschappen van de trainingsdata gebruikt om het netwerk te trainen
  4. een onderbouwing waarom de uitkomst bij de trainingsdata op waarheid berust
Al deze punten vallen onder de term bias.

De Engelse term bias is een homoniem, ofwel één woord met meerdere betekenissen. Het lastige is dat deze verschillende betekenissen op verschillende plaatsen in het ontwikkeltraject van een AI applicatie effect hebben op de fairness van die applicatie. De voor AI belangrijke betekenissen zijn:

  1. bias = vooringenomenheid
  2. bias = vooroordeel
  3. bias = neiging
  4. bias = effect

Al deze betekenissen hebben effect op het design, trainingsdata en training van het netwerk. De eerste twee betekenissen zijn eigenlijk gelijk en zijn van belang in het voortraject van het bouwen van een applicatie. De derde en de vierde betekenis zijn van belang in de beschouwing van de kwaliteit van de trainingsdata.

Maak nu deze belangrijke opdracht
  1. Is er sprake van bias in de "applicaties" die we hebben gemaakt voor de logische schakelingen?
    antwoord
    • Wel degelijk! Één van de auteurs wilde heel graag wat voorbeelden bij elk van de logische schakelingen. De voorbeelden staan stijf van de vooroordelen:
      • In al deze voorbeelden hebben we slechts twee inputs toegestaan: geen andere huisdieren, geen mogelijkheid voor twee jongens, twee meisjes of gender neutrale personen.
      • De beperking in het aantal mogelijke inputs zorgt er voor dat je de applicatie geen voorspelling kan laten doen over situaties die niet in de trainingsdata voorkomen. Dit is een vooroordeel over de mogelijke situaties die we toestaan en die doorwerkt in de bruikbaarheid van een applicatie. Mee te nemen in het traject Rechtvaardiging en verklaarbaarheid
      • Voor de combinaties van input hebben we een uitspraak gedaan over de uitkomst: Wel of niet een dierenliefhebber, wel of niet stapelgek op dieren, wel of niet een verantwoordelijke wereldburger. Deze uitkomst hebben de makers van de applicatie opgelegd als uitkomst van de applicatie en kan een vooringenomenheid zijn.
        Als er niet eerst gedegen onderzoek wordt gedaan naar de waarheid van deze uitkomsten bij de gegeven input dan kan een AI applicatie de reinste onzin produceren. Oorzaak-gevolg relaties worden heel vaak fout gelegd en het is dus zaak te documenteren waar de gebruikte oorzaak-gevolg relatie vandaan komt.

In de opdracht hierboven heb je geleerd dat de aannames die je maakt van groot belang zijn voor de AI applicatie die je maakt. De voorbeelden bij de logische schakelingen zijn heel erg vooringenomen. Er is echter een absolute noodzaak tot vooringenomenheid voor AI applicaties. Een AI applicatie moet voorspellingen kunnen doen, ook in situaties die de applicatie niet eerder heeft gezien. De trainingsdata vormen een landschap. De AI applicatie leert dit landschap op basis van de trainingsdata. Als de applicatie vervolgens een uitspraak moet doen voor een datapunt dat niet gelijk is aan één van de trainingspunten dan gaat de ontwikkelaar van de applicatie er van uit dat dit datapunt en de geleverde voorspelling netjes in dit landschap past.

Op de twee andere betekenissen van bias neiging en effect gaan we dieper in nadat jullie eerst weer wat onderzoek hebben gedaan aan netwerken die moeten leren gebieden te herkennen.


Veel gegevens toch simpel: lijnen

lijn $y=2x-1$ ofwel $x - \frac{1}{2}y= \frac{1}{2}$

In de paragraaf Hoe leert een neuraal netwerk hebben we het leren van een perceptron uitgelegd met behulp van punten die boven (uitvoer = 1) dan wel onder (uitvoer = -1) de lijn $y=2x-1$ liggen. Deze lijn zou bijvoorbeeld een scheidslijn kunnen zijn van twee ondergrondse aardlagen. Om deze grens te bepalen boort men willekeurig gaten in de grond en bepaald men het type van de aardlaag.

In dit voorbeeld en de andere voorbeelden met lijnen bekijken we de invloed van de datapunten op de training van netwerk. De activeringsfunctie die in dit voorbeeld wordt gebruikt is de tangenshyperbolicus functie $tanh(x)$, die waarden tussen -1 en 1 kan aannemen, echter niet de waarden -1 en 1 zelf. Hoe groter (of kleiner) $x$ hoe dichter $\tanh(x)$ bij 1 ( of -1)

Opdrachten

In deze opdrachten maken we weer gebruik van de applet maar nu kies je de optie lijn. Het simpele perceptron netwerk maakt het mogelijk een lijn die de punten scheidt te vinden. Deze lijn valt, afhankelijk van de set trainingspunten, meer of minder samen met de lijn $y=2x-1$. In de vorige paragraaf gebruikten we de teken functie als activeringsfunctie in het trainingsproces. Brain.js heeft deze activeringsfunctie niet. De tangens hyperbolicus functie die ook in de vorige paragraaf is gepresenteerd gebruiken we als alternatief. De tangens hyperbolicus kan ook in netwerken met meer lagen worden gebruikt, waar een 1 of -1 situatie als uitvoer nodig is.

De app in deze pagina kan ook hoger dimensionale netwerken aan (= knopen met meer dan twee elementen in de input lijst). De lijn $y=2x-1$ wordt in deze app weergegeven met $x=x_{1}$ en $y=x_{2}$ als $x_{1} -\frac{1}{2}x_{2}=\frac{1}{2}$

  1. In dit voorbeeld hebben we bewust de fout grens heel tolerant neer gezet en de leersnelheid hoog. Niet altijd, maar vaak, zal na de training van het netwerk een aantal punten aan de verkeerde kant van de door het netwerk berekende lijn liggen. Druk net zo lang op de knop tot er fout voorspelde trainingspunten zijn. In de voorspellingen lijst zijn hebben die punten een rode achtergrond.
    Heb je zo'n situatie gevonden druk dan een aantal malen op de Train knop en bekijk de ligging van de door het netwerk berekende lijn. Is de ligging van de lijn altijd gelijk?
    antwoord
    • Door de grote foutmarge kan het trainen succesvol stoppen zonder alle punten juist te hebben geclassificeerd. Er zullen vele lijnen zijn die binnen deze foutmarge passend zijn.
  2. Wat valt op aan de punten die niet goed voorspeld worden?
    antwoord
    • Deze punten liggen dicht bij de lijn $y=2x-1$.
  3. Verander de fouten grens (threshold) van 0.1 eerst naar 0.01 en dan naar 0.001. Druk dan in die gevallen weer een aantal malen op de Train knop. Wat observeer je in de lijst met voorspellingen en de ligging van de door het netwerk geleverde lijn?
    antwoord
    • Je zult zien dat bij een kleinere toegestane fout de training lijnen oplevert die beter passen en er minder punten fout worden geclassificeerd. De training duurt wel langer.
  4. Zet de grens van de fout weer op 0.1. Verlaag nu de leersnelheid naar 0.1. Onderzoek of dit tot een vergelijkbaar resultaat leidt.
    antwoord
    • In dit voorbeeld heeft het verlagen van de leersnelheid veel minder effect dan het verlagen van de error threshold.

Lijn $y=2x-1$ ofwel $x_{1} -\frac{1}{2}x_{2}=\frac{1}{2}$ met fouten in de trainingsdata

In de situatie hierboven hebben we de invoer zo gemaakt dat de trainingsdata precies vertelde aan welke kant van de werkelijke lijn het punt lag, ofwel we hadden perfecte meetpunten. Nu introduceren we een fout in de metingen. Gebruiken we het voorbeeld van de aardlagen dan kan bij een meetpunt de foute aardlaag worden opgehaald. We nemen aan dat hoe dichter bij de scheidingslijn bent hoe groter de kans is dat een punt een foute uitkomst krijgt. In de simulaties wordt eerst bij toeval een punt gekozen. Dan wordt een toevalsgetal tussen 0 en 1 getrokken. Op basis van dit toevalsgetal en de afstand tot de lijn wordt bepaald of het punt een foute uitvoer krijgt.

Het netwerk weet niet dat die fouten er zijn (weet ook niets van kleurtjes) en gaat proberen de lijn te schatten. Dat lukt niet altijd zoals je in het volgende onderzoekje misschien ziet (Het is en blijft tenslotte een kans proces).

Opdrachten
De simulaties voor deze situatie zijn onder de knop . In het diagram krijgen foute meetpunten een groene kleur en in de lijst van voorspellingen hebben deze punten een groene kleur met zwarte achtergrond als de voorspelling door het netwerk klopt met de foute verwachting en een gele kleur met donkerrode achtergrond als de voorspelling niet in overeenstemming is met de foute verwachting.
  1. Het netwerk onder knop heeft standaard een threshold van 0.1 en een leersnelheid van 0.3. Je hebt bij de lijn situatie al gevonden dat de threshold de belangrijkste instelling is om de lijn zo dicht mogelijk te benaderen.
    Druk nu meerdere malen op de knop. Hoe groot is dan de fout na het stoppen van de training bij de pogingen dat het netwerk niet succesvol eindigt?
    antwoord
    • Die ligt natuurlijk boven de 0.1, maar is vaak behoorlijk veel groter.
  2. Als een training wel lukt, wordt een foutief punt dan ook altijd als een foutief punt gezien (donkerrood) of kan dat punt ook een voorspelling hebben gelijk aan de foute uitvoer waarde (zwarte achtergrond)
    antwoord
    • Heel vaak krijgt een foute uitvoer een vergelijkbare voorspelling. Het netwerk geeft dan eigenlijk een fout antwoord. Maar ja dat weet dat netwerk niet. Het netwerk vindt de voorspelling juist in orde.
  3. Zijn er altijd veel fouten nodig om het trainen te laten mislukken?
    antwoord
    • Soms gaat het al met 1 fout mis, maar met meer foute meetpunten wordt de fout waarbij gestopt wordt groter.
  4. Lukt het om in een situatie waar het trainen misgaat het probleem op te lossen door meer verborgen lagen in te voeren?
    antwoord
    • Het lukt vaak om met een extra verborgen laag [3] een training op een nette manier af te sluiten, meestal wordt de fout bij een mislukte training wel kleiner
  5. Als het lukt om met meer lagen een succesvolle training te krijgen, hoe zit het dan met de voorspelling van de foute punten? Tip: Denk aan het xor voorbeeld.
    antwoord
    • Het kan zo maar zijn dat alle voorspellingen van het netwerk in overeenstemming zijn met de foute invoer (alleen zwarte regels bij de voorspellingen). Waarom is dit te vergelijken met het xor voorbeeld? Bij het xor voorbeeld zijn er minimaal twee lijnen nodig om de gebieden te scheiden. Door de fouten in de trainingsdata onstaan er gebiedjes die door de inzet van meer lijnen afgebakend kunnen worden. Overdimensionering van een netwerk kan dus leiden tot een AI applicatie die alle foutieve voorbeelden goed voorspeld.
  6. Druk weer op de knop en tel in de trainingsdata het aantal fouten. (b.v. 4) Zet lagen op [fouten +2] (b.v. [6]) leersnelheid op 0.1 en threshold op 0.01. Is dit netwerk altijd te trainen?
    antwoord
    • Heel vaak lukt het om dit netwerk te trainen. Doordat er meerdere lijnen worden gevormd kunnen er eilandjes komen waar de fout gemeten punten in komen te liggen. Het netwerk zal dan deze fouten niet corrigeren maar juist accepteren. Klakkeloos een groot netwerk maken om het netwerk goed door een training te laten komen is geen juiste strategie om tot een betrouwbare AI applicatie te komen.
  7. Wat leren we van dit onderzoekje?
    antwoord
    • De kwaliteit van de trainingsdata heeft invloed op het leerproces. Er is een hoge threshold waarde nodig om een netwerk een training netjes af te sluiten. Ook kunnen er meerdere lagen worden ingezet. Het gevolg van beide strategieën is dat het netwerk ver van de echte oplossing kan zijn, waardoor de voorspellende waarde aanzienlijk afneemt en zelfs foutief kan zijn. Best logisch eigenlijk, maar wel een groot punt van aandacht als je een AI applicatie, getraind met kwalitatief slechte trainingsdata, aan gebruikers aanbiedt. De kwaliteit van de trainingsdata heeft invloed op het leerproces. Er is een hoge threshold waarde nodig om een netwerk een training netjes af te sluiten. Ook kunnen er meerdere lagen worden ingezet. Het gevolg van beide strategieën is dat het netwerk ver van de echte oplossing kan zijn, waardoor de voorspellende waarde aanzienlijk afneemt en zelfs foutief kan zijn. Best logisch eigenlijk, maar wel een groot punt van aandacht als je een AI applicatie, getraind met kwalitatief slechte trainingsdata, aan gebruikers aanbiedt.

Bias vervolgd

We hadden beloofd terug te komen op de andere twee betekenissen van bias neiging en effect. In de onderzoekjes naar de kwaliteit van de trainingsdata heb je ervaren dat een lagere threshold waarde, de drempelwaarde van de fout in de training, vaak betere trainingsresultaten levert bij perfecte datapunten, maar dat bij fouten in de trainingsdata een hogere threshold nodig is om een training succesvol af te ronden (onder de voorwaarde dat het netwerk uit dezelfde lagen bestaat). Dit laatste levert dus wel onbetrouwbaarder uitspraken van het netwerk. Als de trainingsdata beter zijn is het effect van de training dus beter en neigt de uitkomst meer naar de waarheid. De bias bepaalt door de trainingsdata wordt dan hoger, in dit geval een positief resultaat. De trainingsdata zijn nu de bepalende factor in de voorspellingen en bepalen nu het vooroordeel. Effect en neiging in het trainingsproces hebben dus als resultaat een vooroordeel door de AI applicatie gegenereerd door de data. 

Je hebt ook gezien dat een netwerk uitgebreid kan worden (overdimensionering) op zo'n manier dat foutieve trainingsdata ook tot een trainingsresultaat kunnen leiden dat het algoritme heel goed vindt en dus een hoge bias levert. De verhoogde bias door overdimensionering is een aanpassing aan foute trainingsdata en dus een aanpassing aan een foute aanname. Het vooroordeel heeft in dit geval dus een negatieve lading.

Kortom het is dus van heel groot belang om de kwaliteit van de trainingsdata vooraf te onderzoeken. Op basis van dit onderzoek moet dan het netwerk worden gevormd.

Vragen
  1. Welke betekenissen heeft het woord bias?
    Antwoord
    • vooringenomenheid, vooroordeel, neiging, effect
  2. Welke betekenissen van bias worden beïnvloed door de keuze van het netwerk en hoe?
    Antwoord
    • neiging, effect. Als de trainingsdata perfect zijn dan kan overdimensionering een positief effect hebben op de kwaliteit van de voorspelling. Het antwoord neigt dan meer naar het juiste antwoord. Bij fouten in de trainingsdata leidt overdimensionering ook tot het voorspellen van die fouten. Dit is een negatief effect.
  3. Hoe kunnen vooringenomenheid en vooroordelen in een een AI applicatie terechtkomen? Geef een voorbeeld.
    Antwoord
    • Garbage in is garbage out! Bij het begeleid leren van een netwerk bestaat de trainingsdata altijd uit vooroordelen. De trainer voorziet het antwoord bij een trainingspunt. Als in de trainingsdata niet alle mogelijke vooroordelen aanwezig zijn, kunnen deze vooroordelen ook niet in het antwoord van de AI applicatie voorkomen. B.v. Als de trainingsdata alleen datapunten bevat van lachende mensen (gelukkig) en huilende mensen (ongelukkig) dan kan het netwerk niet anders dan één van deze twee mogelijkheden als antwoord geven.

Lijnen vervolgd



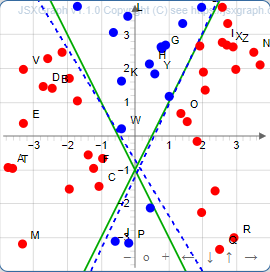
Twee lijnen: De blauwe punten moeten worden gescheiden van de rode punten. De bovenste figuur is de situatie boven 2 lijnen, de onderste figuur de situatie tussen 2 lijnen. De groene lijnen zijn de werkelijke lijnen. De gestippelde blauwe de door training verkregen lijnen.

In het hoofdstuk Hoe een neural netwerk leert hebben we één grens kunnen bepalen tussen een verzameling punten met behulp van één perceptron. Bij het xor (exclusieve-of) voorbeeld hierboven waren er twee lijnen nodig om deze logische schakeling te leren. In dit deel bekijken we puntenverzamelingen die op basis van twee lijnen zijn ingedeeld. We beschouwen twee situaties. Een situatie waarin we het netwerk willen leren een gebied te vinden waar punten zowel boven lijn 1 en boven lijn 2 ligt (boven 2 lijnen). Een tweede situatie waarin we het netwerk willen leren een gebied te vinden waar punten zowel boven lijn 1 en boven lijn 2 ligt of zowel onder lijn 1 en onder lijn 2 ligt (tussen 2 lijnen). De vraag waaraan we hier aandacht besteden is: Hoe ziet het meest minimale netwerk eruit om elk van de twee situaties op te lossen.

Opdrachten

Boven twee lijnen:

  1. Waarom volstaat hier een netwerk met één verborgen laag met twee knopen en één uitvoer knoop?

    antwoord
    • Het probleem kun je vergelijken met twee ja/nee (1/-1) schakelaars. Één schakelaar voor lijn 1 en één schakelaar voor lijn 2. Je weet al dat één perceptron één grens kan leren of wel één schakelaar kan. Als een punt boven lijn 1 ligt moet het antwoord van die perceptron ja (1) evenzo als dat punt boven lijn 1 ligt moet het antwoord van die perceptron ook ja (1) zijn. In andere gevallen moet één van de perceptrons niet het antwoord ja geven.
      De verborgen laag bevat nu die twee schakelaars en deze vormen de input voor de uitvoer knoop net als de en situatie bij de logische schakelingen.
  2. Open weer de applet. Druk in de applet op de knop tot er een situatie is waarbij de training is gelukt.
    1. Overtuig jezelf dat inderdaad het netwerk uit de vorige vraag wordt gebruikt.
      antwoord
      • Druk op het tabblad netwerk.
    2. Bekijk de twee $x_{1},x_{2}$ diagrammen. In het bovenste diagram zie je de toestand van de verborgen laag. Waarom?
      antwoord
      • Je ziet alle ingevoerde punten en die komen uit de invoer. Ook zie je de twee blauw gestippelde lijnen. Dit zijn de door training gevonden lijnen.
    3. In het onderste diagram zie je de toestand van de perceptron uit de uitvoer laag. Je ziet daar vier groepjes punten ongeveer in een vierkant en een lijn. Waar komen die vandaan?
      antwoord
      • Je ziet een groepje dicht bij het punt (1,1), een groepje dicht bij het punt (-1,1), een groepje dicht bij het punt (1,-1) en een groepje dicht bij het punt (-1,-1). Het blauwe groepje hoort bij de punten die boven de twee lijnen liggen. Schuin tegenover dit blauwe groepje bevindt zich een groepje met punten die onder beide lijnen liggen. De andere twee groepjes bevatten punten die boven één van de lijnen liggen en onder de andere.
        Dat de punten zich in die hoeken verzamelen komt door de keuze van de tangenshyperbolicus als activeringsfunctie. Deze functie geeft waarden tussen -1 en 1. Hoe groter de som hoe dichter de waarde bij 1 (of -1 bij negatieve waarde) komt te liggen.
        De blauwe lijn is de grens die door training voor de uitvoer perceptron is gevonden. Deze hoort natuurlijk netjes de blauwe van de rode punten te scheiden.
    4. Druk bij een geslaagde training nog een paar keer op en bekijk de ligging van het groepje blauwe cellen. Ligt dit groepje altijd in de zelfde hoek? Geef een verklaring.
      antwoord
      • Het groepje ligt zeker niet altijd in de zelfde hoek, sterker nog iedere hoek kan het zijn. Verklaring: De gewichten worden bij start van de training willekeurig gekozen. Welke perceptron in de verborgen laag lijn 1 gaat benaderen ligt niet vast. Ook ligt de richting van de lijnen niet vast, daarom kan de input voor de uitvoer perceptron precies andersom zijn. Dus 2x2 is 4 mogelijkheden.
    5. Worden altijd alle trainingsdata goed voorspeld?
      antwoord
      • Niet noodzakelijk, de threshold kan soms gehaald worden met enkele fouten afhankelijk van de waarde van de drempelwaarde (threshold).
  3. Druk op de knop tot er een situatie is waarbij de training mislukt.
    1. Hoeveel punten zijn er niet goed voorspeld?
      antwoord
      • Druk op het tabblad voorspelling. Er moeten zeker fouten zijn.
    2. Druk een paar keer op . Lukt het nu wel?
      antwoord
      • Misschien wel, misschien niet.
    3. Probeer door andere instellingen (lagen, leersnelheid, ...) te kiezen trainingen wel te laten slagen? Wat helpt het best.
      antwoord
      • De leersnelheid verlagen is het meest succesvol, maar wel meer tijdrovend. Meer knopen in de verborgen laag helpt soms ook. Een combinatie van beiden heeft nog meer kans op succes. Denk aan de discussie over bias en het trainen van de logische schakeling excusieve-of.

Tussen twee lijnen:

  1. Waarom volstaat hier een netwerk met één verborgen laag met twee knopen en één uitvoer knoop niet?
    antwoord
    • De toestanden van de twee schakelaars (de geleerde lijnen) moeten in (-1,-1) (beiden onder) of (1,1) beide boven staan. Dit komt overeen met de exclusieve-of logische schakeling. Daar moest een extra verborgen laag worden toegevoegd. Dit moet dus ook in dit geval worden toegevoegd. [2,2] is dan het minimale netwerk, dat nodig is.
  2. Open weer de applet. Druk in de applet op de knop tot er een situatie is waarbij de training is gelukt.
    1. Overtuig jezelf dat inderdaad het netwerk uit de vorige vraag wordt gebruikt.
      antwoord
      • Druk op het tabblad netwerk
    2. Je ziet nu drie $x_{1},x_{2}$ diagrammen. Welke hoort bij welke laag.
      antwoord
      • bovenste->eerste verborgen laag.
        middelste->tweede verborgen laag.
        onderste->uitvoer laag.
    3. Vergelijk de diagrammen met de logische schakeling exclusieve-of (xor). Wat neem je waar?
      antwoord
      • De tweede verborgen laag komt ongeveer overeen met de eerste verborgen laag van de xor trainer.

Eigen Quickdraw vervolgd

In het hoofdstuk technieken heb je gespeeld met een eigen Quickdraw applicatie die je verschillende dieren hebt leren herkennen. Hier stellen we de vraag: Hoe moet een minimaal netwerk er uitzien om $2,3,4,\cdots n$ dieren te leren herkennen. In de eigen Quickdraw applicatie is de input een plaatje bestaande uit zwartwit beeldpunten (pixels). Stel er zijn $n$ beeldpunten.
Opdrachten
  1. Hoeveel inputs zijn er in het netwerk?
    antwoord
    • In het eigen Quickdraw hoofdstuk heb je al gezien dat ieder beeldpunt één input is. Samen met de bias input zijn er dus $n+1$ inputs.
  2. Bewering: Twee dieren leren herkennen is hetzelfde probleem als het leren van de schakelingen of en en en het leren van één scheidingslijn in een verzameling punten.
    Is deze bewering waar of niet waar? Motiveer je antwoord.
    antwoord

    • Deze bewering is waar. De dimensie van de input in een knoop na de input is $n+1$. De input bij de schakeling of en en en de lijn bestond uit een x en een y coördinaat en de 1 voor de bias input dus de dimensie is 3 voor de knoop direct na de input. Een knoop met een input van dimensie 3 moet een rechte lijn leren. Een rechte lijn is een twee dimensionale structuur. Een knoop met dimensie $n + 1$ als input moet een $n$ dimensionale 'lineaire' structuur leren:

      $$w_{0}+w_{1}x_{1}+w_{2}x_{2}+ \cdots + w_{n}x_{n}=0$$

      Een hoger dimensionale lineaire structuur van deze vorm noemt men een hypervlak van dimensie n. Een plaatje als geheel ligt dan boven of onder het te leren hypervlak net als de punten in de voorbeelden van de schakelingen. Neem bijvoorbeeld het leren herkennen van alleen hond of kat. Een kat is dan geen hond. Je hebt dan slechts te leren hond of geen hond. Alle honden plaatjes komen dan aan één kant van het te leren hypervlak, de geen hondjes aan de andere kant.

  3. Wat is het minimale netwerk om twee dieren te leren herkennen?
    antwoord
    • Een enkele output perceptron zou volstaan. Echter de definitie van de output in de plaatjes bij de eigen Quickdraw app is met de naam van het dier. Ieder dier krijgt dan zijn eigen output perceptron. Die perceptrons leren dan direct van de input. Er is geen verborgen laag nodig.
      Gebruik deze versie van de eigen Quickdraw app en train het netwerk met slechts twee diersoorten en geef Deep layers de waarde [].
      Overtuig jezelf dat het getrainde netwerk een goede scheiding geeft tussen de twee diersoorten.
  4. Bewering: Drie dieren leren herkennen (b.v.: kat , hond krokodil ) is hetzelfde probleem als het leren van de het leren van de situatie boven twee lijnen bij een verzameling punten.
    Is deze bewering waar of niet waar? Motiveer je antwoord.
    antwoord
    • Deze bewering is niet helemaal waar, maar komt wel in de buurt. Stel je hebt drie dieren: hond,kat,krokodil. Je kunt dan zeggen dat een krokodil geen kat is en ook geen hond. Als we dan alleen naar kat/geen kat en hond/geen hond kijken dan is het krokodil zijn gelijk aan de situatie geen kat en geen hond ofwel gelijk aan de situatie boven twee lijnen. Er zijn dus twee knopen in de verborgen laag nodig. Het is nu wel noodzakelijk dat ieder dier zijn eigen output knoop heeft.
  5. Welke gebieden in de figuur hieronder horen bij respectievelijk kat, hond en krokodil?

    antwoord
  6. Welke situaties leren de twee knopen in de verborgen laag?

    antwoord
    • In de verborgen laag leert ieder van de twee knopen een hypervlak, dat als grens voor een schakelaar fungeert. Samen vormen de twee knopen in de verborgen laag dus twee schakelaars.
  7. Gebruik weer deze versie van de eigen Quickdraw app en train het netwerk met drie diersoorten en geef Deep layers de waarde [2].
    Overtuig jezelf dat het getrainde netwerk een goede scheiding geeft tussen de drie diersoorten.
  8. Hoewel we bij vraag 5 in één vakje onmogelijk hebben ingevuld kan het netwerk met vier knopen (=diersoorten) in de output laag deze toch gebruiken om dit onlogische vak te gebruiken om de vierde diersoort in te plaatsen. Overtuig jezelf dat je de situatie Deep layers: [2] ook kan gebruiken om vier diersoorten te onderscheiden.
  9. Vermoeden: Voor $n$ diersoorten heb je in de tweede laag minimaal $^{2}\log{n}$ afgerond naar boven knopen in de tweede laag nodig hebt.
    ( $^{2}\log{2}=1$, $^{2}\log{3}=1.58 \rightarrow 2$, $^{2}\log{4}=2, \cdots$, $^{2}\log{8}=3, \cdots$)
    Beargumenteer dat dit waar kan zijn.

    antwoord
    • Een knoop is een schakelaar, met één knoop heb je twee standen voor de schakelaar. Voeg je een knoop ofwel schakelaar toe dan zijn er $2 \cdot 2 = 4$ standen. Een derde knoop geeft dan de mogelijkheid van $2 \cdot 2 \cdot 2= 8$ standen, enzovoorts. Om 8 diersoorten te onderscheiden zou Deep layers: [3] mogelijk moeten zijn.
  10. Is dit minimum aantal ook altijd voldoende? antwoord
    • Het minimum aantal is voldoende als de scheiding tussen de diersoorten altijd lineair is. Is dit niet het geval dan zijn er voor de scheiding meerdere hypervlakken nodig. Vaak worden er dan meerdere verborgen lagen ingezet om het probleem op te lossen.

Je hebt nu kennis gemaakt met neurale netwerken, hoe ze leren, dat bias een probleem is en dat ook de samenstelling van netwerken overdacht moet worden. Meer verdieping willen we je hier niet meer bieden. Misschien heeft deze cursus je nu warm gemaakt voor een studie kunstmatige intelligentie. Wil je geen volledige studie gaan volgen maar wil je toch meer kennis dan zijn er ook nog vele gratis cursussen via universiteiten te volgen. Kijk op Coursera voor een uitgebreid aanbod.In de volgende paragraaf laten we je een hele AI applicatie bouwen. Je ziet dan het hele proces van model naar trainen naar agent op een mobiel.